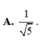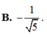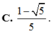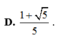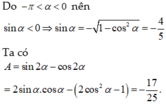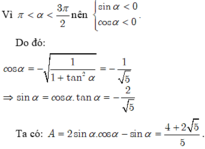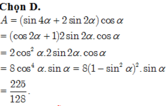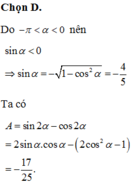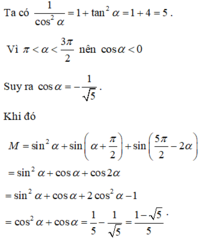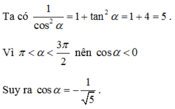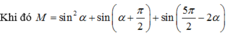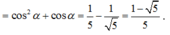Cho cot α =2. Tính giá trị A= sin2α +1 phần 2sin2α+3cos2α

Những câu hỏi liên quan
Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trịcủa các góc nhọn α.a) A cos4α + 2cos2α . sin2α + sin4ab) B sin4α + cos2α . sin2α + cos2αc) C 2(sin α - cos α )2 - (sin α + cos α )2 + 6sin α . cos αd) D (tan α - cot α )2 - (tan α + cot α )2e) E 4 cos2 α + (sin α - cos α)2 + (sin α+ cosα)2 + 2(sin2 α -cos2 α)f) F dfrac{1}{1+sintext{α}}+dfrac{1}{1-sintext{α}}-2 tan2α
Đọc tiếp
Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trị
của các góc nhọn α.
a) A = cos4α + 2cos2α . sin2α + sin4a
b) B = sin4α + cos2α . sin2α + cos2α
c) C = 2(sin α - cos α )2 - (sin α + cos α )2 + 6sin α . cos α
d) D = (tan α - cot α )2 - (tan α + cot α )2
e) E = 4 cos2 α + (sin α - cos α)2 + (sin α+ cosα)2 + 2(sin2 α -cos2 α)
f) F = \(\dfrac{1}{1+sin\text{α}}\)+\(\dfrac{1}{1-sin\text{α}}\)-2 tan2α
Cho góc
α
thỏa mãn
cos
α
3
5
và
-
π
α
0
A
sin
2
α
-
cos
2
α
. Tính giá trị biểu thức .
A
sin
2
α
-
cos
2
α
A.
-
26
25
B.
-
13
25
C. ...
Đọc tiếp
Cho góc α thỏa mãn cos α = 3 5 và - π < α < 0 A = sin 2 α - cos 2 α . Tính giá trị biểu thức . A = sin 2 α - cos 2 α
A. - 26 25
B. - 13 25
C. 3 25
D. - 17 25
cho tam giác ABC vuông tại A, AB<AC, góc C=α<45o, đường trung tuyến AM, đường cao AH, MA=MB=MC=a. c/m:
a) Sin2α=2sinα.cosα
b) 1+cos2α=2cos2α
c)1-cos2α=2sin2α
Cho góc
α
thỏa mãn
π
α
3
π
2
và
tan
α
2
: Tính giá trị của biểu thức
A
sin
2
α
+
cos
α
+
π
2
A.
4
+
2
5
10...
Đọc tiếp
Cho góc α thỏa mãn π < α < 3 π 2 và tan α = 2 : Tính giá trị của biểu thức A = sin 2 α + cos α + π 2
A. 4 + 2 5 10
B. 4 + 5 5 5
C. 4 + 2 5 5
D. 2 + 5 5
Cho
α
là góc thỏa mãn
sin
α
1
4
.Tính giá trị của biểu thức
A
(
sin
4
α
+
2
sin
2
α
)
cos
α
A.
255
128
B.
225
182
C....
Đọc tiếp
Cho α là góc thỏa mãn sin α = 1 4 .Tính giá trị của biểu thức A = ( sin 4 α + 2 sin 2 α ) cos α
A. 255 128
B. 225 182
C. 255 182
D. 225 128
Cho góc
α
thỏa mãn:
cos
α
3
5
v
à
-
π
α
0
.Tính giá trị biểu thức:
A
sin
2
α
-
cos
2
α
A.
-
26
25
B....
Đọc tiếp
Cho góc α thỏa mãn: cos α = 3 5 v à - π < α < 0 .Tính giá trị biểu thức: A = sin 2 α - cos 2 α
A. - 26 25
B. - 13 25
C. 3 25
D. - 17 25
Cho tam giác ABC, AB=AC=1, ^A=2α(0<α<45). Vẽ đường cao AD, BEa) Các tỉ số lượng giác sinα,cosα,sin2α,cos2αđược biểu diễn bởi những đường thẳng nào?b) Chứng minh: tam giác ADC đồng dạng với tam giác BEC, từ đó suy ra các hệ thức:sin2α=2sinαcosαcos2α=1−2sin2α=2cos2α−1=cos2α−sin2α
Cho góc
α
thỏa mãn điều kiện
π
α
3
π
2
và tan
α
2
Tính giá trị của biểu thức
M
sin
2
α
+
sin
α
+
π
2
+
sin...
Đọc tiếp
Cho góc α thỏa mãn điều kiện π < α < 3 π 2 và tan α = 2
Tính giá trị của biểu thức M = sin 2 α + sin α + π 2 + sin 5 π 2 - 2 α
![]()
Cho góc
α
thỏa mãn điều kiện
π
α
3
π
2
và
tanα
2
Tính giá trị của biểu thức M
sin
2
α
+
sin
α
+
π
2
+...
Đọc tiếp
Cho góc α thỏa mãn điều kiện
π < α < 3 π 2 và tanα = 2
Tính giá trị của biểu thức M= sin 2 α + sin α + π 2 + sin 5 π 2 - 2 α