Cho tam giác abc cân tại A có góc A = 30 độ đường cao AH trên cạnh AH lấy điểm M sao cho AM=BC chứng minh rằng tam giác BMC là tam giác đều

Những câu hỏi liên quan
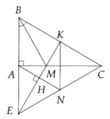
cho tam giác ABC vuông tại A, góc ACB 30 độ. Tia phân giác của góc ABC cắt cạnh AC tại M. Lấy điểm K trên cạnh BC sao cho BABK.a, chứng minh tam giác ABM tam giác KBMb, Gọi E là giao điểm của các đường thẳng AB và KM. Chứng minh tam giác MEC cânc, chứng minh tam giác BEC đềud, Kẻ AH vuông góc EM( H thuộc EM). Các đường thẳng AH và EC cắt nhau tại N. Chứng minh KN vuông góc ới AC
Đọc tiếp
cho tam giác ABC vuông tại A, góc ACB= 30 độ. Tia phân giác của góc ABC cắt cạnh AC tại M. Lấy điểm K trên cạnh BC sao cho BA=BK.
a, chứng minh tam giác ABM= tam giác KBM
b, Gọi E là giao điểm của các đường thẳng AB và KM. Chứng minh tam giác MEC cân
c, chứng minh tam giác BEC đều
d, Kẻ AH vuông góc EM( H thuộc EM). Các đường thẳng AH và EC cắt nhau tại N. Chứng minh KN vuông góc ới AC
a, xét tam giác ABM và tam giác KBM có: AB=BK, BM chung, góc ABM= góc KBM
suy ra 2 tam giác trên bằng nhau
hok tốt
Đúng 0
Bình luận (0)
tu ve hinh :
xet tamgiac ABM va tamgiac KBM co : MB chung
goc ABM = goc MBK do BM la phan giac cua goc ABC (gt)
AB = AK (gt)
=> tammgiac ABM = tamgiac KBM (c - g - c)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông ở A có C=30 độ, đường cao AH. Trên đoạn HC lấy điểm M sao cho HB=HM. chứng minh:
a, AB=AM
b, Tam giác ABM là tam giác đều
c, Từ C kẻ CN vuông góc AM. chứng minh AH=CN
cho tam giác ABC vuông tại A ,có góc C =30 độ , đường cao AH . Trên cạnh BC lấy điểm D sao cho BD=BA . gọi DK là đường cao của tam giác ADC (K thuộc AC ). Chứng minh :
AD là phân giác của góc HAC
tam giác HAK cân
Cho tam giác ABC vuông tại A,
A
C
B
^
30
°
. Tia phân giác của góc ABC cắt cạnh AC tại M. Lấy điểm K trên cạnh BC sao cho BK BA.a) Chứng minh
∆
A
B
M
∆
K
B
M
b) Gọi E là giao điểm của các đường thẳng AB và KM. Chứng minh tam giác MEC cân.c) Chứng minh tam giác BEC đều.d) Kẻ
A
H
⊥
E...
Đọc tiếp
Cho tam giác ABC vuông tại A, A C B ^ = 30 ° . Tia phân giác của góc ABC cắt cạnh AC tại M. Lấy điểm K trên cạnh BC sao cho BK = BA.
a) Chứng minh ∆ A B M = ∆ K B M
b) Gọi E là giao điểm của các đường thẳng AB và KM. Chứng minh tam giác MEC cân.
c) Chứng minh tam giác BEC đều.
d) Kẻ A H ⊥ E M . ( H ∈ E M ) . Các đường thẳng AH và EC cắt nhau tại N. Chứng minh K N ⊥ A C .
Cho tam giác ABC cân tại A có góc A=40 độ và AH là phân giác của góc A. Trên AH lấy E sao cho góc ABE=30 độ, trên AC lấy điểm F sao cho góc CBF=30 độ. Chứng minh tam giác AEF cân
cho tam giác abc vuông tại a có ab=4cm ac=3cm cạnh AC=3cm trên cạnh AB lấy điểm D sao cho AD=AC trên tia dối của tia Ca lấy điểm E sao AE=AB từ A kẻ AH vuông góc với BC và (H E BC) đường thẳng AH cắt DE tại M
a tính độ dài cạnh BC
chứng minh tam giác ABC = tam giác AED từ đó suy ra tam giác ABE là tam giác gì
chứng minh AM là đường trung tuyến của tam giác ADE
a)Áp dụng định lí pytago vào tam giác ABC vuông tại A, ta có
BC^2=AB^2+AC^2
=>BC^2=4^2+3^2
=>BC^2=16+9=25
=>BC=căn25=5 (cm)
vậy,BC=5cm
b)Xét tam giác ABC và AED có
AB=AE(gt)
 là góc chung
AC=AD(gt)
=>tam giác ABC=tam giác AED(c-g-c)
Xét tam giác AEB có:Â=90*;AE=AB
=>tam giác AEB vuông cân tại A
Vậy tam giác AEB vuông cân
c)Ta có EÂM+BÂM=90*
mà BÂM+MÂB=90*
=>EÂM=MÂB
mà MÂB=AÊD(cm câu b)
=>EÂM=AÊD hay EÂM=AÊM
xét tam giác EAM có: EÂM=AÊM(cmt)
=>tam giác EAM cân tại M
=>ME=MA (1)
Ta có góc ACM+CÂM=90*
mà BÂM+CÂM=90*
=>góc ACM=BÂM
mà góc ACM=góc ADM( cm câu b)
=>góc ADM=DÂM
Xét tam giác MAD có góc ADM=DÂM(cmt)
=>tam giác ADM cân tại M
=>MA=MD (2)
Từ (1) và (2) suy ra MA=ME=MD
ta có định lí:trong 1 tam gáic vuông, đg trung truyến ứng với cạnh huyền bằng nửa cạnh huyền
=>MA=1/2ED
=>MA là đg trung tuyến ứng với cạnh ED
Vậy MA là đg trung tuyến của tam giác ADE
Đúng 0
Bình luận (0)
Bài 4: Cho tam giác ABC vuông tại A có đường cao AH, biết AB3cm. AC4cm, trên cạnh AB lấy điểm I sao IA2IB. Đoạn CI cắt AH tại điểm D. Tính dài đoạn thẳng CDBài 5: Cho tam giác đều ABC, điểm M nằm trong tam giác ABC sao cho AM^2BM^2 + CM^2. Tính số đo góc BMCBài 6: Cho hình bình hành ABCD. Trên các cạnh BC và AB ta lấy lần lượt hai điểm M và N sao cho AMCN. Chứng minh SADC SCDN từ đó suy ra D cách đều AM và CN
Đọc tiếp
Bài 4: Cho tam giác ABC vuông tại A có đường cao AH, biết AB=3cm. AC=4cm, trên cạnh AB lấy điểm I sao IA=2IB. Đoạn CI cắt AH tại điểm D. Tính dài đoạn thẳng CD
Bài 5: Cho tam giác đều ABC, điểm M nằm trong tam giác ABC sao cho AM^2=BM^2 + CM^2. Tính số đo góc BMC
Bài 6: Cho hình bình hành ABCD. Trên các cạnh BC và AB ta lấy lần lượt hai điểm M và N sao cho AM=CN. Chứng minh SADC = SCDN từ đó suy ra D cách đều AM và CN
Cho tam giác ABC vuông góc tại A có góc B = 60 độ, kẻ đường cao AH vuông góc với cạnh BC. Trên đoạn HC lấy điểm M sao cho HM = HB. Từ C kẻ CE vuông góc với AM. Chứng minh:
a) Tam giác ABM là tam giác đều
b) Cạnh AH = CE
c) Cạnh EH song song với AC
Mong các bạn giúp mình với !!!
a) Ta thấy :
Xét ∆ABM ta có :
AH là trung trực BM
=>∆ ABM cân tại A
Mà B = 60°
=> ∆ABM đều
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A, góc A = 20 độ. trên AB lấy D sao cho góc BDC = 30 độ. Chứng minh AD=BC.
cho tam giác vuông ABC vuông tại A, đường cao AH. Gọi K,I,J lần lượt là giao điểm của ba đường phân giác ABC, AHB, AHC. Chứng minh AK vuông góc IJ