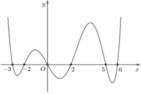
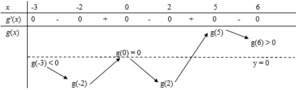
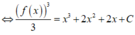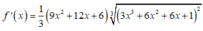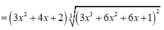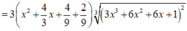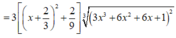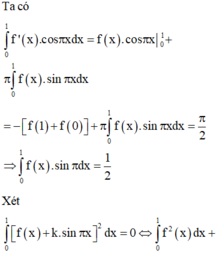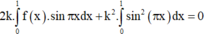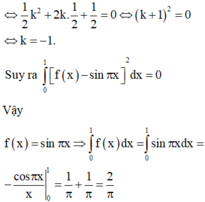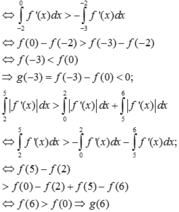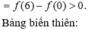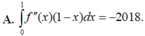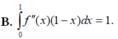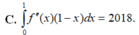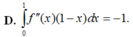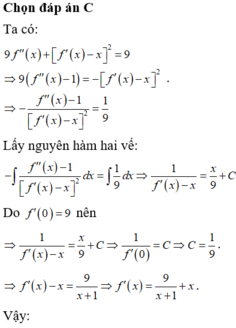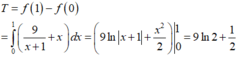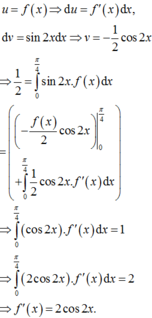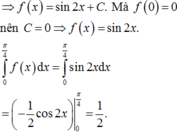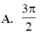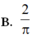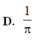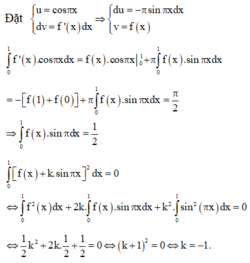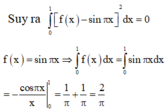1cho hàm số f(x)liên tục trên đoạn [0;10] va\(\int_0^{10}\) f(x)dx=7 và \(\int_2^6\) f(x)dx =3. Tính P=\(\int_0^2\) f(x)dx+\(\int_6^{10}\) f(x)dx
A. P=7 B.P=-4 C.P=4 D.P=10
2 cho f(x) là một nguyên hàm của hàm số y =\(\frac{-1}{cos^2x}\) và f(x)=1. Khi đó , ta có F(x) là
A -tanx B -tanx+1 C tanx+1 D tanx-1
3 Cho A=\(\) \(\int\)x^5.\(\sqrt{1+x^2}\) dx=at^7+bt^5+c^3+C, với t=\(\sqrt{1+x^2}\). Tính A=a-b-c?
4 Tích phân I=\(\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\) \(\frac{dx}{sin^2x}\) bằng
A 1 B 3 C 4 D 2
5 Cho I=\(\int_2^a\) \(\frac{2x-1}{1-x}\)dx, xác định a đề I=-4-ln3
6 diện tích hình phẳng giới hạn bởi các đường cong y=x^3 và y=x^5 bằng
7 Tính thể tích V của khối tròn xoay tạo thành khi ta cho miền phẳng D giới hạn bởi các đường y=sin, trục hoành,x=0, x=\(\frac{\pi}{2}\) quay quanh trục Ox
8 Mô đun của số phức z=\(\frac{z-17i}{5-i}\) có phần thực là
9 cho số phức z thỏa (1-3i)z=8+6i. Mô đun của z bằng
10 phần thực của phức z thỏa (1+i)^2.(2-i)z=8+i+(1+2i)z la
11 cho zố phức z=-1-2i. điểm biểu diễn của số phức z là
A diểm D B diểm B c điểm C D điểm A