Rút gọn biểu thức sau: 2Q=2|x+1|-3|x-1|
Help me. Mai mình phải nộp rồi.
Những câu hỏi liên quan
Rút gọn rồi tính giá trị của biểu thức sau : (x+1).(x^7 - x^6 + x ^5 - x^4 +x^3 - x^2 + x - 1 ) với x= -1 . giải hộ mình nha . chiều nay mình kt 1 tiết rồi . HELP ME !!!
Cho \(abc=2\). Rút gọn biểu thức :
\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
Help me please!
Mai mình phải nộp rồi!
Vì \(abc=2\)nên ta có:
\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{abc.c}{ac+abc.c+abc}\)
\(=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{abc^2}{ac\left(1+bc+b\right)}\)
\(=\frac{1}{bc+b+1}+\frac{b}{bc+b+1}+\frac{bc}{bc+c+1}\)
\(=\frac{1+b+bc}{bc+c+1}=1\)
câu trả lời;
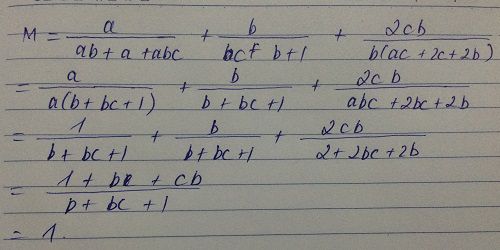
\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(M=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{abc.c}{ac+abc.c+abc}\)
\(M=\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{bc}{1+bc+b}=1\)
Cho A = (1/ x - 2 - 2x/ 4- x^2 + 1/ 2 + x) (2/x - 1)
a, Tìm ĐKXĐ (điều kiện xác định) của A
b,Rút gọn A
c,Tính giá trị của biểu thức A ( sau khi đã rút gọn) tại x thỏa mãn 2x^2 + x = 0
d, Tìm x để A = 1/2
e, Tìm x nguyên để A nguyên dương.
Help me ! Mai mình thi cuối kì 1 môn Toán rồi !
rút gọn biểu thức a và b \:A=\frac{3}{\sqrt{x}-1}+\frac{\sqrt{x\:}-3}{x-1} \:B=\frac{x+2}{x\sqrt{x}-2}-\frac{\sqrt{x}}{\sqrt{x}+2}
b tìm x để A=8/3B
Mình cần gấp mai nộp rồi mình cần gấp
cho biểu thức Q=\(\left(\dfrac{2x+1}{\sqrt{x^3}-1}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\right)\left(\dfrac{1+\sqrt{x^3}}{1+\sqrt{x}}-\sqrt{x}\right)\)với x\(\ge0,x\ne1\)
a) Rút gọn Q
b) tìm x để Q=3
Help me! Mai tớ phải nộp rồi ạ
a) Q=\(\left(\dfrac{2x+1}{\sqrt{x}^3-1}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\right)\left(\dfrac{1+\sqrt{x}^3}{1+\sqrt{x}}-\sqrt{x}\right)\)
=\(\left(\dfrac{2x+1-x+\sqrt{x}}{\sqrt{x}^3-1}\right)\left(\dfrac{1+\sqrt{x}^3-\sqrt{x}-x}{1+\sqrt{x}}\right)\)
=\(\dfrac{\sqrt{x}+x+1}{\sqrt{x}^3-1}.\left(-2\sqrt{x}+1\right)\)
=\(\dfrac{\left(-2\sqrt{x}+1\right)\left(\sqrt{x}+x+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)=\(\dfrac{\left(-2\sqrt{x}+1\right)}{\sqrt{x}-1}\)
b) ta có : Q=3 => \(\dfrac{-2\sqrt{x}+1}{\sqrt{x}-1}=3=>-2\sqrt{x}+1=3\sqrt{x}-3\)
=>x=16/25=0,64
vậy x=0,64 khi Q=3
Đúng 0
Bình luận (2)
a) Q=\(\left(\dfrac{2x+1}{\sqrt{x^3}-1}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\right)\left(\dfrac{1+\sqrt{x^3}}{1+\sqrt{x}}-\sqrt{x}\right)\)
=\(\dfrac{2x+1-\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)-\sqrt{x}\left(1+\sqrt{x}\right)}{1+\sqrt{x}}\)
=\(\dfrac{2x+1-x+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1-\sqrt{x}\right)}{1+\sqrt{x}}\)
=\(\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\left(x-2\sqrt{x}+1\right)\)
=\(\dfrac{\left(x+\sqrt{x}+1\right)\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\sqrt{x}-1\)
b) ta có : Q=3 <=> \(\sqrt{x}-1=3\)
\(\Leftrightarrow\) \(\sqrt{x}=4\Leftrightarrow x=16\)
vậy để Q=3 thì x=16
Đúng 0
Bình luận (0)
Cho biểu thức : Q=\(\frac{\sqrt{x}+2}{\sqrt{x}-3}-\frac{\sqrt{x}+1}{\sqrt{x}-2}-3.\frac{\sqrt{x}-1}{x-5\sqrt{x}+6}\)
a. Tìm điều kiện xác định của Q
b. Rút gọn Q
c. Tìm các giá trị của x để Q<-1
Các bạn gúp mình câu c nha. Mình bí quá. Mai lại phải nộp rồi
Bài 1 : Rút gọn biểu thức sau :
a) A = x + \(|x|\)
b) B = 2. ( 3x - 1) - \(|5-x|\)
Mọi người giúp em vs mai em phải nộp rồi ạ!!
Em cảm ơn !
a)
+) Nếu x > 0 thì A = x + x = 2x
+) Nếu x = 0 thì A = 0 + 0 = 0
+) Nếu x < 0 thì A = -x + x = 0
b) B = 2 ( 3x - 1 ) - | 5 - x |
B = 6x - 2 - | 5 - x |
Xét 3 t/h như câu a)
Đúng 0
Bình luận (0)
a)+) Nếu x > 0 thì A = x + x = 2x
+) Nếu x = 0 thì A = 0 + 0 = 0
+) Nếu x < 0 thì A = -x + x = 0
b) B = 2 ( 3x - 1 ) - | 5 - x |
B = 6x - 2 - | 5 - x |
Xét 3 t/h như câu a)
Đúng 0
Bình luận (0)
1. Rút gọn biểu thức:
\(\sqrt{21-6\sqrt{6}}\)
\(\sqrt{4-\sqrt{7}}\)
\(\sqrt{4+2\sqrt{3}}\)
\(\sqrt{x-2\sqrt{x-1}}\)( x lớn hơn hoặc bằng 1)
Các bạn giúp mình nhé! Ngày mai mình phải nộp rồi! Mình cảm ơn!!!
a)
= \(\sqrt{18-6\sqrt{6}+3}\)
= \(\sqrt{\left(3\sqrt{2}\right)^2-2\cdot3\sqrt{2}\cdot\sqrt{3}+\left(\sqrt{3}\right)^2}\)
= \(\sqrt{\left(3\sqrt{2}-\sqrt{3}\right)^2}\)
= \(|3\sqrt{2}-\sqrt{3}|\)
= \(3\sqrt{2}-\sqrt{3}\)
b)
= \(\sqrt{\frac{7}{2}-\sqrt{7}+\frac{1}{2}}\)
= \(\sqrt{\left(\sqrt{\frac{7}{2}}\right)^2+2\cdot\sqrt{\frac{7}{2}}\cdot\sqrt{\frac{1}{2}}+\left(\sqrt{\frac{1}{2}}\right)^2}\)
= \(\sqrt{\left(\sqrt{\frac{7}{2}}+\sqrt{\frac{1}{2}}\right)^2}\)
= \(|\sqrt{\frac{7}{2}}+\sqrt{\frac{1}{2}}|\)
= \(\sqrt{\frac{7}{2}}+\sqrt{\frac{1}{2}}\)
c)
= \(\sqrt{3+2\sqrt{3}+1}\)
= \(\sqrt{\left(\sqrt{3}\right)^2+2\cdot\sqrt{3}\cdot1+1^2}\)
= \(\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\)
d)
Đặt t = \(\sqrt{x-1}\left(ĐK:t\ge0\right)\)
= \(\sqrt{t^2+1-2t}\)
= \(\sqrt{\left(t+1\right)^2}\)
\(=t+1\)
= \(\sqrt{x-1}+1\)
\(\sqrt{21-6\sqrt{6}}=\sqrt{18-2\sqrt{9}\sqrt{6}+3}=\sqrt{\left(\sqrt{18}\right)^2-2\sqrt{18}\sqrt{3}+\left(\sqrt{3}\right)^2}\)
\(=\sqrt{\left(\sqrt{18}+\sqrt{3}\right)^2}=\sqrt{18}+\sqrt{3}=\sqrt{3}+3\sqrt{2}\)
\(\sqrt{4-\sqrt{7}}=\frac{\sqrt{2}\sqrt{4-\sqrt{7}}}{\sqrt{2}}=\frac{\sqrt{8-2\sqrt{7}}}{\sqrt{2}}=\frac{\sqrt{7-2\sqrt{7}+1}}{\sqrt{2}}\)
\(=\frac{\sqrt{\left(\sqrt{7}-1\right)^2}}{\sqrt{2}}=\frac{\sqrt{7}-1}{\sqrt{2}}=\frac{\sqrt{14}-\sqrt{2}}{2}\)
\(\sqrt{4+2\sqrt{3}}=\sqrt{3+2\sqrt{3}+1}=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\)
Với \(x\ge1\)thì \(\sqrt{x-2\sqrt{x-1}}=\sqrt{\left(x-1\right)-2\sqrt{x-1}+1}\)
\(=\sqrt{\left(\sqrt{x-1}\right)^2-2\sqrt{x-1}\sqrt{1}+\left(\sqrt{1}\right)^2}\)
\(=\sqrt{\left(\sqrt{x-1}-1\right)^2}=\sqrt{x-1}-1\)
T đã tốn mấy phút cuộc đời viết lời giải cho bạn r, tiếc j mấy giây mà bấm k cho t ik =))
Giúp với sáng mai mình nộp rồi
Cho biểu thức: \(\left(\frac{1-x^3}{1-x}+x\right)\left(\frac{1+x^3}{1+x}-x\right)\)
a, Rút gọn A
b,Tìm x để A =64