đề có sai k , lẽ ra DE = 4cm chứ nhỉ

DE là đường trung bình mà nhể => DE = 1/2.BC = 1/2.16 = 4 chứ

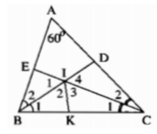
Trong ΔABC, ta có:

∠A +∠B +∠C = 180o (tổng ba góc trong tam giác)

⇒∠B +∠C = 180 - ∠A = 180 - 60 = 120o

+) Vì BD là tia phân giác của ABC nên: ∠(B1 ) = ∠(B2) = 1/2 ∠B

Vì CE là tia phân giác của góc ACB nên: ∠(C1 ) = ∠(C2) = 1/2 ∠ C

Do đó:

Trong ΔBIC, ta có:

∠(BIC) = 180o(∠(B1 ) + ∠(C1) = 180o - 60o = 120o

Kẻ tia phân giác ∠(BIC) cắt cạnh BC tại K

Suy ra: ∠(I2 ) = ∠(I3 ) = 1/2 ∠(BIC) = 60o

Ta có: ∠(I1 ) + ∠(BIC) = 180o (hai góc kề bù)

⇒ ∠(I1 ) = 180o-∠(BIC) = 180o - 120o = 60o

∠(I4 ) = ∠(I1) = 60o(vì hai góc đối đỉnh)

Xét ΔBIE và ΔBIK, ta có

∠(B2) = ∠(B1) (vì BD là tia phân giác của góc ABC)

BI cạnhchung

∠(I1) = ∠(I2) = 60o

Suy ra: ΔBIE = ΔBIK(g.c.g)

IK = IE (hai cạnh tương ứng) (1)

Xét ΔCIK và ΔCID, ta có

∠(C1) = ∠(C2) ( vì CE là tia phân giác của góc ACB).

CI cạnh chung

∠(I3) = ∠(I4) = 60o

Suy ra: ΔCIK = ΔCID(g.c.g)

IK = ID (hai cạnh tương ứng) (2)

Từ (1) và (2) suy ra: IE = ID

1: ΔABD vuông tại D

=>\(\widehat{ABD}+\widehat{BAD}=90^0\)

=>\(\widehat{ABD}+\widehat{BAC}=90^0\left(1\right)\)

ΔACE vuông tại E

=>\(\widehat{ACE}+\widehat{CAE}=90^0\)

=>\(\widehat{ACE}+\widehat{BAC}=90^0\left(2\right)\)

Từ (1) và (2) suy ra \(\widehat{ABD}=\widehat{ACE}\)(3)

2: \(\widehat{ABD}+\widehat{DBC}=\widehat{ABC}\)

\(\widehat{ACE}+\widehat{ECB}=\widehat{ACB}\)

mà \(\widehat{ABD}=\widehat{ACE};\widehat{ABC}=\widehat{ACB}\)

nên \(\widehat{DBC}=\widehat{ECB}\)

=>\(\widehat{HBC}=\widehat{HCB}\)

=>ΔHBC cân tại H

=>HB=HC

3: BO là phân giác của góc ABD

=>\(\widehat{ABO}=\dfrac{1}{2}\cdot\widehat{ABD}\left(4\right)\)

CO là phân giác của góc ACE

=>\(\widehat{ACO}=\dfrac{1}{2}\cdot\widehat{ACE}\left(5\right)\)

Từ (3),(4),(5) suy ra \(\widehat{ABO}=\widehat{ACO}\)

\(\widehat{ABO}+\widehat{OBC}=\widehat{ABC}\)

\(\widehat{ACO}+\widehat{OCB}=\widehat{ACB}\)

mà \(\widehat{ABO}=\widehat{ACO};\widehat{ABC}=\widehat{ACB}\)

nên \(\widehat{OBC}=\widehat{OCB}\)

=>OB=OC

Xét \(\Delta ABC\)có: \(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^o\)

\(\Rightarrow60^o+\widehat{ABC}+\widehat{ACB}=180^o\)

\(\Rightarrow\widehat{ABC}+\widehat{ACB}=120^o\)

Vì BD là tia p/g của góc B, CE là tia phân giác của góc C

\(\Rightarrow\widehat{IBF}+\widehat{ICF}=\frac{1}{2}\cdot\widehat{ABC}+\frac{1}{2}\cdot\widehat{ACB}\)

                                \(=\frac{1}{2}\cdot(\widehat{ABC}+\widehat{ACB})=\frac{1}{2}\cdot120^o=60^o\)

Xét \(\Delta BIC\)có: \(\widehat{IBF}+\widehat{ICF}+\widehat{BIC}=180^o\)

\(\Rightarrow60^o+\widehat{BIC}=180^o\)          \(\Rightarrow\widehat{BIC}=120^o\)

Ta có: \(\widehat{BIC}+\widehat{BIE}=180^o\)(2  góc kề bù)

\(\Rightarrow120^o+\widehat{BIE}=180^o\)          \(\Rightarrow\widehat{BIE}=60^o\)

Vì IF là tia phân giác của góc BIC

\(\Rightarrow\widehat{BIF}=\widehat{CIF}=\frac{1}{2}\cdot\widehat{BIC}=\frac{1}{2}\cdot120^o=60^o\)

\(\Rightarrow\widehat{BIE}=\widehat{BIF}\)

Xét \(\Delta BIE\)và \(\Delta BIF\)có:

     \(\widehat{EBI}=\widehat{FBI}\)(BD là tia phân giác của góc B)

      BI là cạnh chung

       \(\widehat{BIE}=\widehat{BIF}\left(cmt\right)\)

\(\Rightarrow\Delta BIE=\Delta BIF\left(g.c.g\right)\)

=> IE = IF (2 cạnh tương ứng) (1)

Ta có: \(\widehat{BIE}=\widehat{CID}=60^o\)(2 góc đối đỉnh)

\(\Rightarrow\widehat{CID}=\widehat{CIF}\)

Xét \(\Delta CID\)và \(\Delta CIF\)có:

     \(\widehat{DCI}=\widehat{FCI}\)(CE là tia p/g của góc ACB)

     CI là cạnh chung

      \(\widehat{CID}=\widehat{CIF}\left(cmt\right)\)

\(\Rightarrow\Delta CID=\Delta CIF\left(g.c.g\right)\)

=> ID = IF (2 cạnh tương ứng) (2)

Từ (1) và (2) => ID = IE

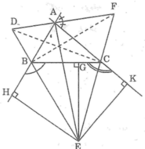
Ta có: AE là tia phân giác góc trong tại đỉnh A

      AF là tia phân giác góc ngoài tại đỉnh A

Suy ra: AE ⊥ AF (tính chất hai góc kề bù)

Vậy AE ⊥ DF.