Cho m,a,b∈Z thỏa m=a-b
Biết rằng m>0 chọn câu đúng
A. a>b
B. a<b
C.a=b
D.a≤b
Chọn câu đúng . Với a; b; m ∈ Z; m ≠ 0 ta có :
A. a m + b m = a - b m
B. a m + b m = a . b m
C. a m + b m = a + b m
D. a m + b m = a + b m + m
Đáp án là C
Muốn cộng hai phân số cùng mẫu, ta cộng các tử và giữ nguyên mẫu
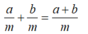
Chọn câu đúng. Với a;b;m ∈ Z; ,m ≠ 0 ta có
A. a m + b m = a − b m
B. a m + b m = a . b m
C. a m + b m = a + b m
D. a m + b m = a + b m + m
Đáp án cần chọn là: C
Muốn cộng hai phân số cùng mẫu, ta cộng các tử và giữ nguyên mẫu.
a m + b m = a + b m
Giả sử x = \(\dfrac{a}{m}\), y = \(\dfrac{b}{m}\)(a, b, m \(\in\) Z, m > 0) và x < y. Hãy chứng tỏ rằng nếu chọn z = \(\dfrac{a+b}{2m}\) thì ta có x < z < y
Hướng dẫn: Sử dụng tính chất: Nếu a, b, c \(\in\) Z và a < b thì a + c < b + c
Giúp mk nốt câu này nhé
câu 1
giả sử x=a/m, y=b/m( a,b,m thuộc Z m>0) và x<y. chúng tỏ rằng nếu chọn z=a+b/2m thì ta có x<z<y
câu 2
a,chứng tỏ rằng nếu a/b<c/d (b>0, d>0") thì a/b<a+c/b+d<c/d
b, hãy viết 3 số hữu tỉ xen giữa -1/3 và -1/4
cậu tra trên google ấy , **** tớ cái nha !
nếu ko thấy trên googlle thì để tớ giúp nhưng cậu phải **** cho tớ đã
Giả sử, x=a/m, y=b/m (với a,b, m thuộc Z, m>0) Chọn Z=a+b/2m.Chứng tỏ rằng nếu x<Z<y.
Giả sử x = \(\dfrac{a}{m}\); y = \(\dfrac{b}{m}\)(a;b;m ϵ Z, m ≠ 0 và x < y). Hãy chứng tỏ rằng nếu chọn z = \(\dfrac{a+b}{2m}\) thì x < y < z.
1) So sánh số hữu tỉ a/b (a,b thuộc Z, b khác 0) vs số 0 khi a,b cùng dấu và khi a,b khác dấu.
2) Giả sử x=a/m, y=b/m (a,b,m thuộc Z, m>0) và x>y.Hãy chứng tỏ rằng nếu chọn z=a+b/2m thì ta có x<z<y. ( sử dụng tính chất: nếu a,b,m thuộc Z và a<b thì a+m<b+m)
1) Với a, b ∈ Z, b> 0
- Khi a , b cùng dấu thì \(\frac{a}{b}\) > 0
- Khi a,b khác dấu thì \(\frac{a}{b}\)< 0
Tổng quát: Số hữu tỉ \(\frac{a}{b}\) ( a,b ∈ Z, b # 0) dương nếu a,b cùng dấu, âm nếu a, b khác dấu, bằng 0 nếu a = 0
Theo đề bài ta có x = a/m, y = b/m (a, b, m ∈ Z, b # 0)
Vì x < y nên ta suy ra a < b
Ta có: x = 2a/2m, y = 2b/2m; z = (a+b)/2m
Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z < y
 ( m là hằng số, m ≠ 0 )D. Cả A và B đều đúng
( m là hằng số, m ≠ 0 )D. Cả A và B đều đúngGiả sử x=a/m, y=b/m(a,b,m thuộc Z, m>0) với số 0 khi a, b cùng dấu và x<y. Hãy chứng tỏ rằng nếu chọn z=a+b/2m thì ta có x<z<y