Cho tam giác ABC có a lớn hơn 120 độ phía ngoài tam giác ABC tính các tam giác đều ABD và AC AB đường thẳng qua d song song AD cắt nhau tại f a Chứng minh AD = EF B Chứng minh tam giác b f c đều thừa nhận card + be + ADV + dab = 360 độ

Những câu hỏi liên quan
Bài 1: Cho ΔABCΔABC có Aˆ900A^900, AB AC. Vẽ đường cao AH của tam giác ABC. Trên tia HC lấy điểm D sao cho HD HA. Đường thẳng vuông góc với BC tại D cắt AC tại E. Vẽ EF⊥AHEF⊥AH tại F.a) CMR: EF DH.b) CMR: AB AE và tính số đo các góc của tam giác ABE.c) Đường trung trực của đoạn DE cắt BE ở M. Chứng minh các tam giác DME cân và DMB cân.d) Tính AHMˆAHM^ (thừa nhận EHAˆ+EHBˆ+BHAˆ3600EHA^+EHB^+BHA^3600)Bài 2: Cho tam giác đều ABC. Trên tia AC lấy điểm D (ADAC) vẽ tam giác đều ADE (B, E thuộc hai...
Đọc tiếp
Bài 1: Cho ΔABCΔABC có Aˆ=900A^=900, AB > AC. Vẽ đường cao AH của tam giác ABC. Trên tia HC lấy điểm D sao cho HD = HA. Đường thẳng vuông góc với BC tại D cắt AC tại E. Vẽ EF⊥AHEF⊥AH tại F.
a) CMR: EF = DH.
b) CMR: AB = AE và tính số đo các góc của tam giác ABE.
c) Đường trung trực của đoạn DE cắt BE ở M. Chứng minh các tam giác DME cân và DMB cân.
d) Tính AHMˆAHM^ (thừa nhận EHAˆ+EHBˆ+BHAˆ=3600EHA^+EHB^+BHA^=3600)
Bài 2: Cho tam giác đều ABC. Trên tia AC lấy điểm D (AD>AC) vẽ tam giác đều ADE (B, E thuộc hai nửa mặt phẳng đối nhau bờ AD). Tia EC cắt BD ở M.
a) CMR: BD = CE.
b) Trên tia ME lấy F sao cho MF = MD. CMR tam giác MDF đều.
c) Chứng minh ME = MD + MA, MA = MB + MC
Bài 3: Cho tam giác ABC có Aˆ>1200A^>1200. Phía ngoài tam giác ABC, vẽ các tam giác đều ABD, ACE. Đường thẳng qua D song song với AE và đường thẳng qua E song song với AD cắt nhau tại F.
a) CMR: AD = EF
b) Chứng minh tam giác BFC đều (thừa nhận BACˆ+CAEˆ+EADˆ+DABˆ=3600BAC^+CAE^+EAD^+DAB^=3600)
giải nhanh giúp mình nhé, cảm ơn ạ!
Cho tam giác ABC có góc A = 120 độ, đường phân giác AD (D thuộc BC). Vẽ DE vuông góc với AB, DF vuông góc với AC. a)tam giác DEF là tam giác gì?. b) Lấy K nằm giữa E và B, lấy I nằm giữa F và C sao cho EK = FI. Chứng minh tam giác DKI cân tại D. c) Từ C kẻ đường thẳng song song với AD cắt AB tại M. Chứng minh tam giác AMC đều. d) Tính DF biết AD = 4 cm
https://lazi.vn/edu/exercise/cho-tam-giac-abc-co-goc-a-120-do-duong-phan-giac-ad-d-thuoc-bc-ve-de-vuong-goc-voi-ab-df-vuong-goc
a) ΔAED=ΔAFDΔAED=ΔAFD(ch-gn)nên DE=DF.(hai cạnh tương ứng)
Mặt khác dễ dàng chứng minh được EDFˆ=60o
Vì vậy tam giác DEF là tam giác đều
b)ΔEDK=ΔFDT(hai cạnh góc vuông)
nen DK=DI(hai cạnh tương ứng).Do đó Tam giác DIK cân ở D
c) AD là tia phân giác của góc BAC nên DAB^=DAC^=1/2BAC^=60o
AD//MC(gt),do đó AMCˆ=DABˆ=60o(hai góc nằm trong vị trí đồng vị)
AMC^=CAD^=60o(hai góc nằm trong vị trí sole trong)
Tam giác AMC có hai góc bằng nhau và khoảng 60o nên là tam giác đều
d)Ta có AF=AC-FC=CM-FC=m-n.
Cho tam giác ABC có góc A=120 độ, phân giác AD lần lượt cắt AB; AC ở E và F. Trên EB và FC lấy các điểm K và I sao cho EK=FI
a) Chứng minh tam giác DEF đều
b) Chững minh tam giác DIK cân
c) Từ C kẻ đường thẳng song song với AD cắt tia BA tại M
Chứng minh tam giác MAC đều. Tính AD theo CM=m và CF=n
Cho tam giác ABC có góc A = 120 độ, đường phân giác AD, D thuộc BC. Từ D hả DE vuông góc AB, DK vuông goác AC.
a)Chứng minh: tam giác DHK là tam giác đều
b) Qua C kẻ đường thẳng song song AD cắt AB ở I. Chứng minh: tam giác ACI là tam giác đều
Cho tam giác ABC. Vẽ AH vuông góc BC (H thuộc BC). Về phía ngoài tam giác ABC vẽ các tam giác ABD và ACE vuông cân tại A. Đường thẳng AH cắt DE tại M.a) Chứng minh: BD^2+CE^22.(AB^2+AC^2)2.BH^2+4.AH^2+2.CH^2b) Vẽ DP vuông góc AH tại P, EQ vuông góc AH tại Q. Chứng minh AP BHc) Chứng minh M là trung điểm của DEd) Đường thẳng qua D song song với AE và đường thẳng qua E song song với AD cắt nhau tại F. Chứng minh F, A, H thẳng hàng.
Đọc tiếp
Cho tam giác ABC. Vẽ AH vuông góc BC (H thuộc BC). Về phía ngoài tam giác ABC vẽ các tam giác ABD và ACE vuông cân tại A. Đường thẳng AH cắt DE tại M.
a) Chứng minh: BD^2+CE^2=2.(AB^2+AC^2)=2.BH^2+4.AH^2+2.CH^2
b) Vẽ DP vuông góc AH tại P, EQ vuông góc AH tại Q. Chứng minh AP = BH
c) Chứng minh M là trung điểm của DE
d) Đường thẳng qua D song song với AE và đường thẳng qua E song song với AD cắt nhau tại F. Chứng minh F, A, H thẳng hàng.
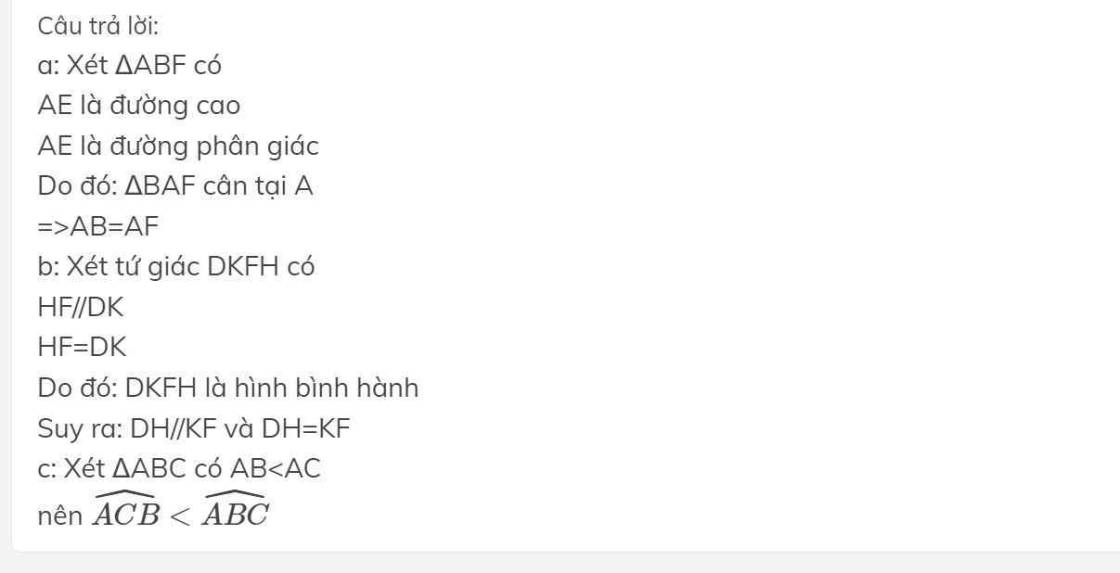
Cho tam giác ABC có các góc đều nhọn và AB < AC. Phân giác góc A cắt cạnh BC tại D. Vẽ BE vuông góc với AD tại E. Tia BE cắt cạnh AC tại F
a)Chứng minh AB = AF
b) Qua F vẽ đường thẳng song song với BC , cắt AE tại H lấy điểm K nằm giữa D và C sao cho FH = DK. Chứng minh: DH = KF và DH song song với KF
c) Chứng minh: Góc ABC lớn hơn góc C
Nguyen Phan Cam Chau cậu làm được chưa
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc m, phân giác AD. Từ D kẻ những đường thẳng vuông góc với AB và AC, lần lượt cắt AB, AC ở E và F. Trên EB và FC lấy các điểm K và I sao cho EK = FI.
a) Chứng minh tam giác DEF đều.
b) Chứng minh tam giác DIK cân.
c) Từ C kẻ đường thẳng song song với AD cắt tia BA tại M. Chứng minh tam
giác MAC đều. Tính AD theo CM = m và CF = n
Sửa đề △ABC có ^CAB = 120o thì mới chứng minh △DEF đều được.
a, Xét △FDA vuông tại F và △EDA vuông tại E
Có: DA là cạnh chung
^FAD = ^EAD (gt)
=> △FDA = △EDA (ch-gn)
=> DF = DE (2 cạnh tương ứng)
=> △DEF cân tại D (1)
Vì AD là phân giác ^CAB => ^CAD = ^BAD = ^CAB : 2 = 120o : 2 = 60o
Xét △FAD vuông tại F có: ^FAD + ^FDA = 90o (tổng 2 góc nhọn trong tam giác vuông)
=> 60o + ^FDA = 90o => ^FDA = 30o
Mà ^FDA = ^EDA (△FDA = △EDA) => ^EDA = 30o
Ta có: ^FDE = ^FDA + ^EDA = 30o + 30o = 60o (2)
Từ (1) và (2) => △DEF đều
b, Ta có: AI = AF + FI và AK = AE + EK
Mà AF = AE (△FDA = △EDA) ; FI = EK (gt)
=> AI = AK
Xét △IAD và △KAD
Có: AI = AK (cmt)
^IAD = ^KAD (gt)
AD là cạnh chung
=> △IAD = △KAD (c.g.c)
=> ID = KD (2 cạnh tương ứng)
=> △IDK cân tại D
c, AD // CM (gt) => ^DAB = ^CMB (2 góc đồng vị)
Mà ^DAB = 60o => ^CMB = 60o => ^CMA = 60o (3)
Ta có: ^CAM + ^CAB = 180o (2 góc kề bù)
=> ^CAM + 120o = 180o => ^CAM = 60o (4)
Từ (3) , (4) => ^CMA = ^CAM => △CMA cân tại C mà ^CMA = 60o => △MAC đều
=> AC = AM = MC
Vì △ vuông FAD có: ^FDA = 30o (cmt)
=> AD = 2 . AF
=> AD = 2 . (AC - CF)
=> AD = 2 . (CM - CF) = 2 . (m - n)
CHO TAM GIÁC ABC CÓ A=100 ĐỘ VÀ AB=AC. TRÊN TIA AB LẤY D SAO CHO AD=BC. TRÊN BC LẤY E SAO CHO BAE=60 ĐỘ . QUA B VẼ ĐƯỜNG THẲNG SONG SONG VỚI AC CẮT AE TẠI F. CHỨNG MINH
A,TAM GIÁC ADF ĐỀU
B, TAM GIÁC AEB= TAM GIÁCCEF
C, TAM GIÁC ADC= TAM GIÁC FDC
D, TÍNH SỐ ĐO GÓC ADC
a, Ta có: AB=AC => tg ABC cân tại A
=>\(\widehat{B_1}=\widehat{C_1}=\frac{180^o-100^o}{2}=40^o\)
BF//AC => \(\widehat{B_2}=\widehat{C_1}=40^o\left(slt\right);\widehat{BFA}=\widehat{CAF}\left(slt\right)\)
Mà \(\widehat{CAF}=\widehat{BAC}-\widehat{BAE}=100^o-60^o=40^o\)
=>\(\widehat{B_2}=\widehat{BFA};\widehat{C_1}=\widehat{CAF}\)
=> tg EFB cân tại E ; tg EAC cân tại E
=> EF=EB ; EA=EC
=>EF + EA = EB + EC
Mà E nằm giữa F,A và B,C
=> AF = BC mà BC=AD (gt)
=>AF = AD
=> tg ADF cân tại A
Mà góc DAF = 60 độ (gt)
=>tg ADF đều
Nối C với D nhé
b, xét tg ABE và tg CFE có:
BE=FE (cm câu a)
góc AEB = góc CEF (đối đỉnh)
AE=CE (cm câu a)
=>tg ABE = tg CFE (c.g.c)
c, từ câu b => góc ABE = góc CFE = 40 độ (2 góc t.ứ)
=> góc DFC = góc AFD + góc EFC = 60 độ + 40 độ = 100 độ
Xét tg ACF có: góc ECA = góc EFC (=40 độ)
=>tg ACF cân tại C => AC = FC
Xét tg ADC và tg FDC có:
góc DAC = góc DFC (=100 độ)
AD = FD (tg ADF đều)
AC = FC (cmt)
=>tg ADC = tg FDC (c.g.c)
Xem thêm câu trả lời
Cho tam giác ABC có các góc đều nhọn với AD tại E, tia BE cắt AC tai F. Qua F vẽ đường thẳng song song với BC, đường thẳng này cắt AE tại H. Lấy điểm K nằm giữa D và C sao cho FH=DK. Nối D với F
a,Chứng minh: tam giác ABE = tam giác AFE
b,Chứng minh: DH=KF và DH//KF