1, Gọi số đó là :a

=>a-3⋮4,6,8

=>a-3 ϵ\(\left\{24,48,72,96,120,...\right\}\)

=>a ϵ\(\left\{27,51,75,99,123,...\right\}\)

Vì a là số nhỏ nhất có 3 chữ số thỏa mãn đề bài nên a=123.

Tìm kiếm bài học, bài tập, mã lớp, mã khóa học...

hehe

Theo đề bài ta có : a/(11/18) = a*(18/11) thuộc N suy ra 18*a chia hết cho 11.

                  Lại có : a/(25/6) = a*(6/25) thuộc N suy ra 6*a chia hết cho 25.

Như vậy, a là bội chung của 11 và 25 nhưng để a nhỏ nhất thì a = BCNN (11, 25) = 275.

Vậy số cần tìm là 275 bạn nhé!

Chúc bạn học tốt!

hiii mong bạn hiểu

a, Gọi số phải tìm là a, a ∈ N*

Vì a chia cho 6, 7, 9 được số dư lần lượt là 2, 3, 5 nên (a+4) chia hết cho 6,7,9.

Suy ra (a+4) ∈ BC(6,7,9)

Mà a là số tự nhiên nhỏ nhất

Suy ra (a+4) = BC(6,7,9) =  3 2 . 2 . 7 = 126 => a+4 = 126 => a = 122

Vậy số phải tìm là 126

b, Gọi số phải tìm là a, a ∈ N*

Vì a chia  cho 17, 25 được các số dư theo thứ tự là 8 và 16.

nên (a+7) chia hết cho 8; 16.

Suy ra (a+7) ∈ BC(8;16)

Suy ra BCNN(8;16) = 16 => a+7 ∈ B(16) = 16k (k ∈ N).

Vậy số phải tìm có dạng 16k – 7

Các số nguyên tố là các số tự nhiên lớn hơn 1 chỉ có 2 ước là 1 và chinh nó

=> n không bằng 1

Là số 7.

a) Vì  nên (n + 1) ∈ Ư(6) = {1; 2; 3; 6}

Ta có bảng sau:

Vì n là số tự nhiên nên n ∈ {0; 1; 2; 5}

Vậy n ∈ {0; 1; 2; 5}.
b) Gọi x = 23.3a  và y = 2b.35

Ta có tích của hai số là tích của ƯCLN và BCNN của hai số đó.

Ta có: x. y = ƯCLN(x, y). BCNN(x, y)

Vì ước chung lớn nhất của hai số là   và bội chung nhỏ nhất của hai số là 23.36.

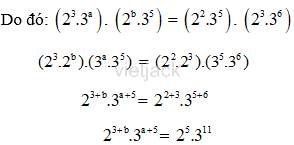
Vì thế 3 + b = 5. Suy ra b = 5 – 3 = 2

         a + 5 = 11. Suy ra a = 11 – 5 = 6

Vậy a = 6; b = 2.

Gọi x = 2³.3^a  và y = 2^b.3⁵

Ta có: x. y = ƯCLN(x, y). BCNN(x, y)

Vì ước chung lớn nhất của hai số là 2².3⁵ và bội chung nhỏ nhất của hai số là 2³.3⁶

Ta được x.y= 22.35.23.36=22.23.35.36=25.31122.35.23.36=22.23.35.36=25.311

Mà xy =23+b.3a+523+b.3a+5

Ta được 5=3+b và 11=a+5

Vậy b=2 và a=6