Cho tứ giác ABCD diện tích S. Điểm M là trung điểm của AC. Chứng minh rằng ![]() . Sabcd=1/2S
. Sabcd=1/2S

Những câu hỏi liên quan
Cho tứ giác ABCD có diện tích là S. Điểm M là trung điểm của AC. Chứng minh S A B M D = 1 2 S .
Chứng minh:
SABMD = SABM + SADM.
= 1 2 S A B C + 1 2 S A D C = 1 2 S A B C D
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. E là giao điểm của AB và CD. Gọi F là trung điểm của AC, G là trung điểm của BD. Chứng minh diện tích tam giác EFG = 1/4 diện tích tứ giác ABCD.
Cho tứ giác lồi ABCD có diện tích S và O là điểm nằm trong tứ giác sao cho OA^2+OB^2+OC^2+OD^2=2S. Chứng minh rằng ABCD là hình vuông có tâm là O
cho tứ giác ABCD. Gọi O là giao điểm của các đường thẳng nối trung điểm những cạnh đối diện. chứng minh rằng
SAOD + SBOC = 1/2 SABCD
Cho tứ giác lồi ABCD , E và F theo thứ tự là trung điểm của cạnh AB,AD.Gọi G=AE giao BF, H=CF giao BD. chứng minh rằng diện tích EFGH = SABC+SDHCNếu M,N nằm trên hai cạnh còn lại của tứ giác sao cho MENF là hình chữ nhật SMENF =SABCD
cho tứ giác abcd gọi m,n lần lượt là trung điểm của ab và dc, đường chéo ac cắt mn tại trung điểm i của mn, chứng minh diện tích tam giác abc bằng diện tích tam giác adc
Cho tam giác ABC. Gọi M,N là các trung điểm tương ứng của AB, AC
a) Chứng minh rằng tứ giác BMNC là hình thang
b) Gọi P là trung điểm của BC. Chứng minh rằng tứ giác BMNP là hình bình hành
c) Biết diện tích tam giác AMN bằng 2 cm2 . Tính diện tích tam giác ABC.
Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt trung điểm của AB, CD, BC, AD, AC và BD. Chứng minh rằng tứ giác MNPQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
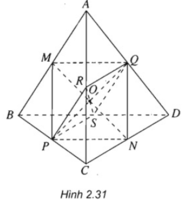
Trong tam giác ABC ta có:
MP // AC và MP = AC/2.
Trong tam giác ACD ta có:
QN // AC và QN = AC/2.
Từ đó suy ra {MP // QN}
⇒ Tứ giác MNPQ là hình bình hành.
Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O của mỗi đường.
Tương tự: PR // QS và PR = QS = AB/2. Do đó tứ giác PQRS là hình bình hành.
Suy ra hai đường chéo RS và PQ cắt nhau tại trung điểm O của PQ và OR = OS
Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt là trung điểm của AB, CD, BC, AD, AC và BD. Chứng minh rằng tứ giác MPNQ là hình bình hành. Từ đó suy ra 3 đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn ?
Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của AC và BD. I là giao điểm của AD và BC. Gọi M, N lần lượt là trung điểm của AB và CD. a) Chứng minh rằng I, M, O, N thẳng hàng b) Giả sử CD=3AB và diện tích hình thang ABCD bằng a, Hãy tính diện tích tứ giác IAOB theo a















