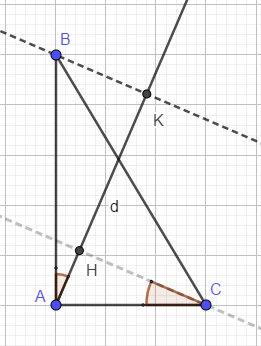
1. Cho tam giác vuông cân ABC, \(\widehat{A}=90^0\). Qua A kẻ đường thẳng d tùy ý. Từ B và C kẻ BH ⊥ d, CK ⊥ d. Chứng minh rằng tổng \(BH^2+CK^2\) không phụ thuộc vào vị trí của đường thẳng d.
2. Cho tam giác vuông ABC, \(\widehat{A}\) = \(90^0\). Trên nửa mặt phẳng bờ AC không chứa điểm B, kẻ tia Cx sao cho CA là tia phân giác của góc BCx. Từ A kẻ AE ⊥ Cx, từ B kẻ BD ⊥ AE. Gọi AH là đường cao của tam giác ABC.
a) Chứng minh rằng: A là trung điểm của DE.
b) \(\widehat{DHE}\) = \(90^0\).