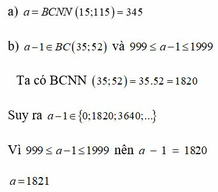Tìm a biết a là số tự nhiên lôn nhất thỏa mãn 3,6 *a<15

Những câu hỏi liên quan
Tìm a là một số tự nhiên thỏa mãn điều kiện sau
2,9 × 3,6 < a < 5,2 × 2,1
\(2,9\cdot3,6< a< 5,2\cdot2,1\)
\(10,44< a< 10,92\)
Mà a là số tự nhiên => không có giá trị phù hợp cho a
2,9 × 3,6 < a < 5,2 × 2,1
<=> 10.44 < a < 10.92
=> Đề sai ạ mong bạn xem lại
ko có số tự nhiên nào phù hợp
Tìm số tự nhiên M nhỏ nhất có 4 chữ số thỏa mãn : M= a+b=c+d=e+f
Biết rằng a,b,c,d,e,f là các số tự nhiên khác 0 thỏa mãn a/b = 14/22 , c/d = 11/13 , e/f = 13/17
Ta có:
\(\frac{a}{b}=\frac{14}{22}=\frac{14k}{22k}=>a=14k,b=22k=>M=a+b=14k+22k=36k\)
\(\frac{c}{d}=\frac{11}{13}=\frac{11m}{13m}=>c=11m,d=13m=>M=c+d=11m+13m=24m\)
\(\frac{e}{f}=\frac{13}{17}=\frac{13n}{17n}=>e=13n,f=17n=>M=e+f=13n+17n=30n\)
=>M=36k=24m=30n
=>M chia hết cho 36,24,30
Ta thấy: ƯCLN(36,24,30)=360
=>M chia hết cho 360
=>M=360h
mà M là số bé nhất có 4 chữ số=>h bé nhất
=>999<360h
=>2<h
mà h bé nhất
=>h=3
=>M=3.360=1080
Vậy M=1080
Đúng 1
Bình luận (0)
$\frac{a}{b}=\frac{14}{22}=\frac{14k}{22k}=>a=14k,b=22k=>M=a+b=14k+22k=36k$
Đúng 0
Bình luận (0)
Số tự nhiên a lớn nhất thỏa mãn 75 ⋮ a và 100 ⋮ a là:
Số tự nhiên a nhỏ nhất thỏa mãn 20 ⋮ a và 35 ⋮ a là:
Tìm số tự nhiên a, biết rằng:
a) a là số nhỏ nhất khác 0 thỏa mãn a ⋮ 15 và a ⋮ 115
b) a - 1 ⋮ 52 , a - 1 ⋮ 35 và 1000 < a < 2000
Tìm số tự nhiên a lớn nhất thỏa mãn điều kiện: 12.5 x a < 2010
Trả lời: Số tự nhiên a cần tìm là ...........
Số tự nhiên lớn nhất mà a cần tìm là : 25125
Chúc bạn học tốt nha !
Đúng 0
Bình luận (0)
ồ,sao bạn lại nói vậy hả,Nguyễn Vũ Dương?
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm số tự nhiên a lớn nhất thỏa mãn điều kiện: 12,5xa<2010
Trả lời: Số tự nhiên a cần tìm là
a là 160 nhé.
Vì 12,5 x 160 = 2000 < 2010
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm số tự nhiên a lớn nhất thỏa mãn điều kiện: 12,5xa<2010
Trả lời: Số tự nhiên a cần tìm là
ta thấy:2010:12,5=160,8
=>số tự nhiên a lớn nhất là 160
Đúng 0
Bình luận (0)
tìm số tự nhiên a lớn nhất thỏa mãn điều kiện 12,5xa<2010
số tự nhiên cần tìm là
số tự nhiên cần tìm là:12,5*160<2010
BẠN NHỚ TK CHO MÌNH NHA
Đúng 0
Bình luận (0)
bằng 160.7
tk mk nha mọi người , ủng hộ với
Đúng 1
Bình luận (0)
Đáp số:160
Đúng 100% luôn
Ai tk mình mình tk lại
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm số tự nhiên a, biết rằng:a, a là số nhỏ nhất khác 0 thỏa mãn a chia hết cho 15 và 115b, a – 1 chia hết cho 52; a – 1 chia hết cho 35 và 1000 a 2000
Đọc tiếp
Tìm số tự nhiên a, biết rằng:
a, a là số nhỏ nhất khác 0 thỏa mãn a chia hết cho 15 và 115
b, a – 1 chia hết cho 52; a – 1 chia hết cho 35 và 1000 < a < 2000
a, a = BCNN(15;115) = 345
b, a – 1 ∈ BC(35;52) và 999 < a – 1 < 1999
Ta có BCNN(35;52) = 35.52 = 1820
Suy ra a – 1 ∈ {0;1820;3640;...}
Vì 999 < a – 1 < 1999 nên a – 1 = 1820
a = 1821
Đúng 0
Bình luận (0)