Cho tam giác ABC có góc BAC= 90 độ.Tính AD biết CD=7,DB=18,AD=AB

Những câu hỏi liên quan
Cho hình vẽ AB//CD, AD//BC,AD=BC,AB=DC chứng minh tam giác ABC=tam giác CDA cho góc D=60 độ.tính góc B
Xét ΔABC và ΔCDA có
AB=CD
\(\hat{BAC}=\hat{DCA}\) (hai góc so le trong, AB//CD)
AC chung
Do đó: ΔABC=ΔCDA
=>\(\hat{ABC}=\hat{CDA}\)
=>\(\hat{ABC}=60^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB < AC, AD là tia phân giác của góc BAC (Dthuộc BC). Chứng minh rằng:
a) góc ADB < góc ADC;
b) CD > DB.
Tại sao mà nói AD là tia phân giác rồi mà còn CD > DB ????
Cho tam giác ABC có AB< AC, AD là tia phân giác của góc BAC (D€ BC) Chứng minh rằng
a,Góc ADB< góc ADC
b, CD> DB
a) Trong \(\Delta ABC\),do AB < AC(gt) nên \(\widehat{C}< \widehat{B}\)(góc đối diện với cạnh lớn hơn là góc lớn hơn)
\(\widehat{ADB},\widehat{ADC}\)theo thứ tự là góc ngoài tại đỉnh D của \(\Delta ADC,\Delta ADB\) ta có :
\(\hept{\begin{cases}\widehat{ADB}=\widehat{C}+\widehat{A_1}\left(1\right)\\\widehat{ADC}=\widehat{B}+\widehat{A_2}\left(2\right)\end{cases}}\)
Vì \(\widehat{C}< \widehat{B}\),còn \(\widehat{A_1}=\widehat{A_2}\)(gt) , do đó từ 1 và 2 => \(\widehat{ADB}< \widehat{ADC}\)
b) Do AB < AC(gt),trên cạnh AC lấy điểm E sao cho AE = AB
Xét \(\Delta ADB\) và \(\Delta ADE\)có :
AD chung
\(\widehat{DAB}=\widehat{DAE}\)
AB = AE(gt)
=> \(\Delta ADB=\Delta ADE\left(c.g.c\right)\)
Nên \(\widehat{AED}=\widehat{B}\) mà \(\widehat{AEB}+\widehat{DEC}=180^0\)(2 góc kề bù),do đó \(\widehat{B}+\widehat{DEC}=180^0\left(3\right)\)
Mặt khác \(\Delta ABC\)thì \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\), do đó \(\widehat{B}+\widehat{C}< 180^0\left(4\right)\)
Từ 3 -> 4 ta có \(\widehat{DEC}>\widehat{C}\)
Trong \(\Delta DEC\)ta có DE < DC,nhưng DE = DB(cạnh tương ứng của hai tam giác bằng nhau : \(\Delta ADB=\Delta ADE\))
Vậy DB < DC hay DC > DB
Cho tam giác ABC có AB< AC, AD là tia phân giác của góc BAC (D€ BC) Chứng minh rằng
a,Góc ADB< góc ADC
b, CD> DB
a, Xét △ABD và △ACD có:
AB=AC(gt)AB=AC(gt)
Aˆ1=Aˆ2A^1=A^2 (vì AD là phân giác của ∠A)
AD chung
⇒ΔABD=ΔACD(c.g.c)⇒ΔABD=ΔACD(c.g.c)
Vậy ΔABD=ΔACD(đpcm)ΔABD=ΔACD(đpcm)
b, Vì △ABD=△ACD (chứng minh trên) nên ta có:
Bˆ=CˆB^=C^ (hai góc tương ứng)
Vậy Bˆ=Cˆ(đpcm)B^=C^(đpcm)
c, Vì △ABD=△ACD (chứng minh trên) nên ta có:
Dˆ1=Dˆ2D^1=D^2 (hai góc tương ứng)
Mà Dˆ1+Dˆ2=1800D^1+D^2=1800 (kề bù)
⇒Dˆ1=Dˆ2=18002=900⇒D^1=D^2=18002=900
Vậy AD⊥BC(đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB< AC, AD là tia phân giác của góc BAC (D thuộc BC). Chứng minh rằng
a,Góc ADB< góc ADC
b,CD> DB
Cho ∆ABC có AB < AC, AD là tia phân giác của góc BAC (DBC).Chứng minh CD>DB
Cho tam giác ABC có AD là tia phân giác của góc BAC. Biết AB = 3cm, BD = 4cm, CD = 6cm. Tính AC?
A. 4cm
B. 5cm
C. 6cm
D. 4,5cm
Theo tính chất tia phân giác của góc ta có:
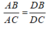
Suy ra:

Chọn đáp án D
Đúng 0
Bình luận (0)
bài1: cho tam giác abc, đường phân giác ad chia cạnh đối diện thành các đoạn bd2 cm; cd 4 cm. đường trung trực của ad cắt đường thẳng bc tại k. tính kdbài 2: cho tam giác abc và đường cao ah, ab 5cm, bh3cm, acfrac{20}{3}cm. tính góc bacbài 3: ch tứ giác abcd, có góc dbc900 , ad sqrt{20}cm, ab 4 cm, db 6cm, dc9 cm. CMR dc//ab
Đọc tiếp
bài1: cho tam giác abc, đường phân giác ad chia cạnh đối diện thành các đoạn bd=2 cm; cd= 4 cm. đường trung trực của ad cắt đường thẳng bc tại k. tính kd
bài 2: cho tam giác abc và đường cao ah, ab= 5cm, bh=3cm, ac=\(\frac{20}{3}\)cm. tính góc bac
bài 3: ch tứ giác abcd, có góc dbc=900 , ad = \(\sqrt{20}cm\), ab= 4 cm, db= 6cm, dc=9 cm. CMR dc//ab
Cho tam giác ABC có AD là đường phân giác của góc A biết AB = 6 cm AC = 8 cm CD = 4 cm Tính dB
Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{6}=\dfrac{4}{8}=\dfrac{1}{2}\)
=>\(BD=\dfrac{6}{2}=3\left(cm\right)\)
Đúng 0
Bình luận (0)


















