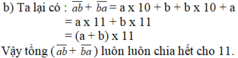Cho ba số ab ; ac ; ba có bội chung là abc. Chứng minh rằng abc cũng là bội của bc.

Những câu hỏi liên quan
Cho 2 số có 2 chữ số: a là chữ số hàng chục và b là chữ số hàng đơn vị, sẽ được viết là ab. Giả sử aba, em hãy chứng tỏ rằng hiệu ( ab - ba ) luôn luôn chia hết cho 9.c, chứng tỏ rằng tổng ( ab + ba ) luôn luôn chia hết cho 11. Số ba la số viết ngược lại của số ab
Đọc tiếp
Cho 2 số có 2 chữ số: a là chữ số hàng chục và b là chữ số hàng đơn vị, sẽ được viết là ab. Giả sử a>b
a, em hãy chứng tỏ rằng hiệu ( ab - ba ) luôn luôn chia hết cho 9.
c, chứng tỏ rằng tổng ( ab + ba ) luôn luôn chia hết cho 11. Số ba la số viết ngược lại của số ab ![]()
tìm số tự nhiên ab ( gạch ngang trên đầu), sao cho : ab- ba = 72 ( ab và ba có gạch ngang trên đầu, ab và ba là hai số tự nhiên)
ab - ba = 72
ax10 + b - bx10 - a = 72
ax9 - bx9 = 72
a - b = 8
Mà a,b là các chữ số
=> a = 8 , b = 0
Hoặc a = 9 , b = 1
Vậy các SCT là 91 và 80
Tham khảo ạ ~
Đúng 0
Bình luận (0)
Cho 2 số có 2 chữ số: a là chữ số hàng chục và b là chữ số hàng đơn vị, sẽ được viết là ab. Giả sử a>ba
Em hãy chứng tỏ rằng hiệu ( ab - ba ) luôn luôn chia hết cho 9.
Chứng tỏ rằng tổng ( ab ba ) luôn luôn chia hết cho 11. Số ba là số viết ngược lại của số ab.
a) Ta có : ab - ba
= ( 10 x a + b ) - ( 10 x b + a )
= ( 10 x a - a ) - ( 10 x b - b )
= 9 x a - 9 x b
= 9 x ( a - b )
\(\Rightarrow\)ab - ba chia hết cho 9
b) Ta có: ab + ba
= ( 10 x a + b ) + ( 10 x b + a )
= ( 10 x a + a ) + ( 10 x b + b )
= 11 x a + 11 x b
= 11 x ( a + b )
\(\Rightarrow\)ab + ba chia hết cho 11
Nhớ k chị nha. Chúc em học tốt.
Đúng 2
Bình luận (0)
a)Ta có:
ab-ba =a.10+b-b.10-a
=a.9-b.9
Mà a > b nên thương nhỏ nhất của hai số sẽ bằng 9.
=> ab-ba luôn chia hết cho 9
b) ab+ba =a.10+b+b.10+a
=a.11+b.11
=(a+b).11
=> ab+ba luôn chia hết cho 11
Đúng 0
Bình luận (0)
???????????????????
Cho 2 số có 2 chữ số: a là chữ số hàng chục và b là chữ số hàng đơn vị, sẽ được viết là ab. Giả sử a>b
a, em hãy chứng tỏ rằng hiệu ( ab - ba ) luôn luôn chia hết cho 9.
c, chứng tỏ rằng tổng ( ab + ba ) luôn luôn chia hết cho 11. Số ba la số viết ngược lại của số ab.
c, Ta có ab+ba = 10a + 10b + a + b=11a + 11b
Vậy ab+ba chia hết cho 11
Đúng 0
Bình luận (0)
Tìm số nguyên tố 'ab' sao cho 'ba' cũng là số nguyên tố và 'ba' - 'ab' là số chính phương
11 hoặc 12 nhỉ
ab=11 , ba =11 mà ba-ab=11-11=0 0=0^2
ab=12 , ba =21 mà ba-ab=21-12=9 9=3^2
mới thử thôi , chắc ko phải tất cả
Đúng 0
Bình luận (0)
Tím số có hai chữ số khác nhau dạng ab sao cho ba là số nguyên tố và ab - ba là số chính phương
ab-ba=10a+b-10b-a=9a-9b=9(a-b) là số chính phương
=>a-b là số chính phương
=>a-b=1;4
xét a-b=1=>ba=23=>ab=32
a-b=4=>ba=37=>ab=73
vậy ab=32;73
Đúng 0
Bình luận (0)
Tớ muốn hỏi bài của bạn là tại sao a-b=1 mà suy ra ba=23.Bạn nói ko có căn cứ
Đúng 0
Bình luận (0)
Tìm các chữ số a và b sao cho :
a) ab+ba chia hết cho 7 (ab và ba có gạch trên đầu)
b) ab+ba chia hết cho 15 (ab và ba có gạch trên đầu)
c) Cho biết số abc chia hết cho 7. CMR: 2a+3b+c chia hết cho 7 ( abc có gạch trên đầu nhưng 2a ; 3b ; c không có gạch trên đầu)
Tìm một số tự nhiên có hai chữ số có dạng ab, sao cho (ba.10):ab=45 (tất cả các số ab;ba đều có gạch trên đầu)
Lời giải:
$\overline{ba}.10=\overline{ab}.45$
$(10b+a).10=(10a+b).45$
$100b+10a = 450a+45b$
$55b = 440a$
$5b=40a$
$\Rightarrow 40a=5b< 5.10<80$
$\Rightarrow a< 2$
Mà $a$ là số tự nhiên khác 0 nên $a=1$.
$5b=40.a=40\Rightarrow b=8$.
Vậy số cần tìm là $18$
Đúng 0
Bình luận (0)
Tìm số có 2 chữ số khác nhau ab sao cho ba cũng là số nguyên tố và hiệu ab-ba là số chính phương
Cho một số có 2 chữ số: a là chữ số hàng chục và b là chữ số hàng đơn vị, số được viết là
a
b
¯
. Giả sử a bb) Chứng tỏ rằng tổng (
a
b
¯
+
b
a
¯
) luôn luôn chia hết cho 11. Số
b
a...
Đọc tiếp
Cho một số có 2 chữ số: a là chữ số hàng chục và b là chữ số hàng đơn vị, số được viết là a b ¯ . Giả sử a > b
b) Chứng tỏ rằng tổng ( a b ¯ + b a ¯ ) luôn luôn chia hết cho 11. Số b a ¯ là số viết ngược lại của số a b ¯ .