|x|+1\3=1\1phần 3

Những câu hỏi liên quan
Tính giá trị nhỏ nhất của các biểu thức sau:
1.A= /2x-1phần 5/+173
2.B=/x+1phần 2/+?x+1phần 3/+/x+1phần 4/ (ko có dấu giá trị tuyệt đối ^.^b)
1 phần 1×3 + 1phần 2×4 + 1phần 3×5+.......+1phần +98×100
Bài làm:
Ta có: \(\frac{1}{1.3}+\frac{1}{2.4}+\frac{1}{3.5}+...+\frac{1}{98.100}\)
\(=\left(\frac{1}{1.3}+\frac{1}{3.5}+...+\frac{1}{97.99}\right)+\left(\frac{1}{2.4}+\frac{1}{4.6}+...+\frac{1}{98.100}\right)\)
\(=\frac{1}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{97}-\frac{1}{99}\right)+\frac{1}{2}\left(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+...+\frac{1}{98}-\frac{1}{100}\right)\)
\(=\frac{1}{2}\left(1-\frac{1}{99}\right)+\frac{1}{2}\left(\frac{1}{2}-\frac{1}{100}\right)\)
\(=\frac{1}{2}.\frac{98}{99}+\frac{1}{2}.\frac{49}{100}\)
\(=\frac{49}{99}+\frac{49}{200}\)
\(=\frac{14651}{19800}\)
7/48 - ( 1 phần 2 x 2 + 1phần 4x 3 + 1 phần 6x 4 + 1phần 8 x 5 + 1 phần 10 x 6 + 1 phần 12 x 7 + 1 phần 14 x 8 ) : x= 0
7/48 - (1/2 x 2 + 1/6 x 4 + 1/8 x 5 + 1/12 x 7 + 1/14 x 8) : x = 0
7/48 - (1 + 2/3 + 5/8 + 7/12 + 4/7) : x = 0 (đã rút gọn)
7/48 - (336/336 + 224/336 + 210/336 + 196/336 + 192/336) : x = 0 (quy đồng)
7/48 - 193/56 : x = 0
193/56 : x = 0 + 7/48
193/56 : x = 7/48
x = 193/56 : 7/48
x = 1158/49
Cho B = 1phần 2 +(1phần 2 mũ 2)+(1phần 2 mũ 3) +.......+(1phần 2mũ 98) +(1phần 2 mũ 99)
Chứng minh rằng B<1
\(B=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{98}}+\dfrac{1}{2^{99}}\\ =\left(2-1\right)\cdot\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{98}}+\dfrac{1}{2^{99}}\right)\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{2^2}+\dfrac{1}{2^2}-\dfrac{1}{2^3}+...+\dfrac{1}{2^{98}}-\dfrac{1}{2^{99}}\\ =1-\dfrac{1}{2^{99}}< 1\)
Vậy \(B< 1\)
Đúng 0
Bình luận (0)
\(B=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{98}}+\dfrac{1}{2^{99}}\)
\(\Rightarrow2B=2\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{98}}+\dfrac{1}{2^{99}}\right)\)
\(\Rightarrow2B=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{97}}+\dfrac{1}{2^{98}}\)
\(\Rightarrow2B-B=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{97}}+\dfrac{1}{2^{98}}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{98}}+\dfrac{1}{2^{99}}\right)\)
\(\Rightarrow B=1-\dfrac{1}{2^{99}}\)
\(\rightarrow B< 1\rightarrowđpcm\)
Đúng 0
Bình luận (0)
Cho em hỏi bài sau
a,x+1phần 3=2 phần 5 - [-1 phần 3]
b, 5 phần 7 -x=1 phần 4-[-3 phần 5]
x+\(\frac{1}{3}\)=\(\frac{2}{5}\)- (\(\frac{-1}{3}\))
x + \(\frac{1}{3}\)= \(\frac{2}{5}\)+\(\frac{1}{3}\)
x +1/3 =11/15
x= 11/15 -1/3
x= 2/5
b, 5/7-x=1/4 -(-3/5)
5/7 - x = 1/4 +3/5
5/7 - x =17/20
x = 5/7 -17/ 20
x= -19/140
Đúng 0
Bình luận (0)
cho biểu thức p=(1 phần 11 -x phần 1-x^3*x^2+x+1 phần x+1* 2x+1phần x^2 +2x +1 a,tìm điều kiện xác định của p
1phần 3<x<1phần 2
tìm giá trị lớn nhất của biểu thức sau
D = 1phần 2./ x - 1 / + 3
\(D=\dfrac{1}{2\left|x-1\right|+3}\)
\(\left|x-1\right|\ge0\Rightarrow2\left|x-1\right|\ge0\Rightarrow2\left|x-1\right|+3\ge3\)
\(D=\dfrac{1}{2\left|x-1\right|+3}\le\dfrac{1}{3}\)
Dấu "=" xảy ra khi:
\(x=1\)
Đúng 0
Bình luận (0)
Cho hàm số y = -3x
a) Vẽ đồ thị hàm số
b)Đặt y =f(x) =-3. Tính f(1phần 3),f(1),f(-1phaaanf)
a)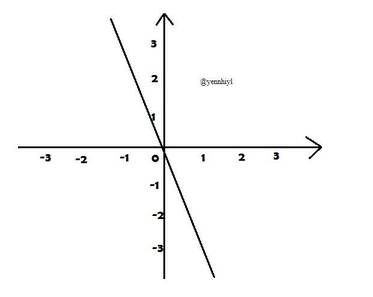
b) \(f\left(\dfrac{1}{3}\right)=-3.\dfrac{1}{3}=-1\)
\(f\left(1\right)=-3.1=-3\)
\(f\left(-1\right)=-3.-1=3\)
Đúng 0
Bình luận (0)


















