Chứng tỏ rằng : Tích (2017n+2019)*(2017n+2018) chia hết cho 2

Những câu hỏi liên quan
Chứng tỏ rằng :
Tích ( 2017n + 2019 )( 2017n + 2018 ) Chia hết cho 2
# Mk sẽ tick #
Xét tích nếu n lẻ \(\Rightarrow2017n+2019\)là chẵn . \(2017n+2018\)là lẻ
\(\Rightarrow\left(2017n+2019\right)\left(2017n+2018\right)=\)chẵn . lẻ \(=\)chẵn
\(\Rightarrow\left(2017n+2019\right)\left(2017n+2018\right)⋮2\)
Xét tích nếu n chẵn \(\Rightarrow2017n+2019\)là lẻ . \(2017n+2018\)là chẵn
\(\Rightarrow\left(2017n+2019\right)\left(2017n+2018\right)=\)lẻ. chẵn\(=\)chẵn
\(\Rightarrow\left(2017n+2019\right)\left(2017n+2018\right)⋮2\Rightarrowđpcm\)
Nếu n là số chẵn suy ra 2017n chẵn suy ra 2017n+2018 là số chẵn suy ra (2017n+2019)(2017n+2018) chia hết cho 2
Nếu n là số lẻ suy ra 2017n lẻ suy ra 2017n+2019 chẵn suy ra (2017n+2019)(2017n+2018) chia hết cho 2
Cho 2017m-2018<2017n-2018 , hãy so sánh m và n
\(2017m-2018< 2017n-2018\)
\(\Leftrightarrow\)\(2017m< 2017n\) (cộng thêm 2 vế với 2018)
\(\Leftrightarrow\)\(m< n\) (nhân cả 2 vế với 1/2017 > 0 nên ko đổi chiều)
Vậy \(m< n\)
p/s: hk tốt
Đúng 0
Bình luận (0)
Tìm x thuộc N* biết 2017n^2+2017n+13 chia hết cho n+1
Xem chi tiết
tìm tất cả các số nguyên n để p=2017n^2+2015n+30 chia hết cho 6n
chứng tỏ rằng 2019^2018-1 chia hết cho 2018
noooooooooooooooooooooooooooooooooo mếu làm được
Đúng 0
Bình luận (0)
Gọi S là tập các số nguyên của a sao cho
l
i
m
4
n
2
+
2017
n
-
2018
-
a
n
có giá trị hữu hạn. Tính tổng các phần tử của S. A. S 4 B. S 0 C. S 2 D. S 1
Đọc tiếp
Gọi S là tập các số nguyên của a sao cho l i m 4 n 2 + 2017 n - 2018 - a n có giá trị hữu hạn. Tính tổng các phần tử của S.
A. S = 4
B. S = 0
C. S = 2
D. S = 1
Chọn C.
- Ta có:
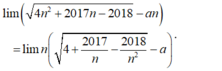
- Vì:
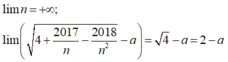
- Suy ra:  có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.
có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.
Đúng 0
Bình luận (0)
Gọi S là tập các số nguyên của a sao cho
l
i
m
4
n
2
+
2017
n
-
2018
-
a
n
có giá trị hữu hạn. Tính tổng các phần tử của S. A. S 4 B. S 0 C. S 2 D. S 1
Đọc tiếp
Gọi S là tập các số nguyên của a sao cho l i m 4 n 2 + 2017 n - 2018 - a n có giá trị hữu hạn. Tính tổng các phần tử của S.
A. S = 4
B. S = 0
C. S = 2
D. S = 1
Chọn C.
- Ta có:
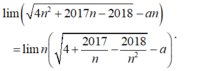
- Vì:
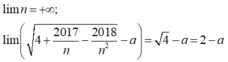
- Suy ra:  có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.
có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.
Đúng 0
Bình luận (0)
Số tự nhiên n phải thỏa mãn điều kiện gì để biểu thức sau chia hết cho 3:
M=2017n+2017n+n2017
Xét :
+) \(n=3k\left(k\in N\right)\)
Ta có: \(M=2017^{3k}+2017.3k+\left(3k\right)^{2017}⋮3\)
<=> \(2017^{3k}⋮3\)vô lí vì \(2017:3\)dư 1 nên \(2017^{3k}:3\)dư 1
+) \(n=3k+1\left(k\in N\right)\)
Ta có: \(M=2017^{3k+1}+2017.\left(3k+1\right)+\left(3k+1\right)^{2017}\equiv1+1+1\equiv0\left(mod3\right)\)
=> \(M⋮3\)
+) \(n=3k+2\left(k\in N\right)\)
Ta có: \(M=2017^{3k+2}+2017.\left(3k+2\right)+\left(3k+2\right)^{2017}\equiv1+2+2^{2017}\equiv1+2+\left(-1\right)^{2017}\equiv2\left(mod3\right)\)
=> \(M⋮̸3\)
Vậy n = 3k +1 ( k là số tự nhiên ) thì M chia hết cho 3.
B = 1+ 2018 + 20182 +20183 +... Chứng tỏ B chia hết cho 2019
















