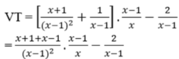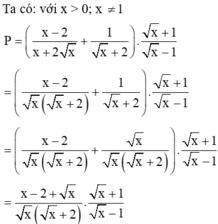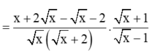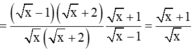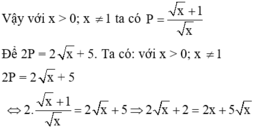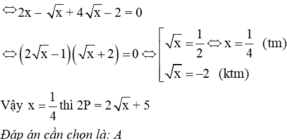2914^(x-1).2x=1x

Những câu hỏi liên quan
Chứng minh rằng:
x
+
1
x
-
2
x
+
1
+
1
x
-
1
:
x
x
-
1
-...
Đọc tiếp
Chứng minh rằng:
x + 1 x - 2 x + 1 + 1 x - 1 : x x - 1 - 2 x - 1 = 0
Cho biểu thức
P
x
-
2
x
+
2
x
+
1
x
+
2
.
x
+
1...
Đọc tiếp
Cho biểu thức P = x - 2 x + 2 x + 1 x + 2 . x + 1 x - 1
với x > 0; x ≠ 1.
Tìm x để 2P = x + 5
A. x = 1 4
B. x = 1 2
C. x = 4
D. x = 2
Giải các phương trình sau:a)
x
−
2
x
+
x
x
+
2
2
;
b)
2
x
+
1
−
1
x
−
2
3...
Đọc tiếp
Giải các phương trình sau:
a) x − 2 x + x x + 2 = 2 ;
b) 2 x + 1 − 1 x − 2 = 3 x − 11 x + 1 x − 2 ;
c) 5 + 96 x 2 − 16 = 2 x − 1 x + 4 + 3 x − 1 x − 4 ;
d) 2 x + 2 − 2 x 2 + 16 x 3 + 8 = 5 x 2 − 2 x + 4 .
Giải phương trình
a
)
2
x
+
3
x
-
4
2
x
-
1
x
+
2
-
27
b
)
x
2
-
4
-
x
+
5...
Đọc tiếp
Giải phương trình
a ) 2 x + 3 x - 4 = 2 x - 1 x + 2 - 27
b ) x 2 - 4 - x + 5 2 - x = 0
c ) x + 2 x - 2 - x - 2 x + 2 = 4 x 2 - 4
d ) x + 1 x - 1 - x + 2 x + 3 + 4 x 2 + 2 x - 3 = 0
a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27
⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27
⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29
⇔ -2x – 3x = 24 – 29
⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1
Tập nghiệm của phương trình : S = {1}
b) x2 – 4 – (x + 5)(2 – x) = 0
⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0
⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0
⇔ x = 2 hoặc x = -7/2
Tập nghiệm của phương trình: S = {2; -7/2 }
c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)
⇔ x ≠ 2 và x ≠ -2
Quy đồng mẫu thức hai vế :
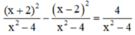
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4
⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {1/2}
d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)
⇔ x ≠ 1 và x ≠ -3
Quy đồng mẫu thức hai vế :
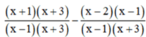
![]()
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0
⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = ∅
Đúng 0
Bình luận (0)
\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)
\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)
\(< =>2x^2-2x-24=2x^2+3x-2-27\)
\(< =>5x=-24+29=5\)
\(< =>x=\frac{5}{5}=1\)
\(x^2-4-\left(x+5\right)\left(2-x\right)=0\)
\(< =>\left(x-2\right)\left(x+2\right)+\left(x+5\right)\left(x-2\right)=0\)
\(< =>\left(x-2\right)\left(x+2+x+5\right)=0\)
\(< =>\left(x-2\right)\left(2x+7\right)=0\)
\(< =>\orbr{\begin{cases}x-2=0\\2x+7=0\end{cases}}< =>\orbr{\begin{cases}x=2\\x=-\frac{7}{2}\end{cases}}\)
Xem thêm câu trả lời
Tập nghiệm của phương trình
x
-
1
x
+
1
-
x
+
1
x
-
1
2
x
+
3
x
2
-
1
là: A.
S...
Đọc tiếp
Tập nghiệm của phương trình x - 1 x + 1 - x + 1 x - 1 = 2 x + 3 x 2 - 1 là:
A. S = 1 2
B. S = - 1 2
C. S = 2 3
D. S = 3 2
Chứng minh đẳng thức:
2
3
x
-
2
x
+
1
x
+
1
3
x...
Đọc tiếp
Chứng minh đẳng thức: 2 3 x - 2 x + 1 x + 1 3 x - x - 1 : x - 1 x = 2 x x - 1
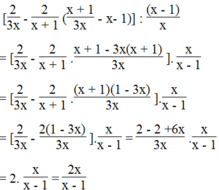
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
x
+
2
x
−
2
2
x
x
−
2
+
1
x
;
b)
5
x
−...
Đọc tiếp
Giải các phương trình sau:
a) x + 2 x − 2 = 2 x x − 2 + 1 x ;
b) 5 x − 2 3 − x + x + 3 2 − x = 0 ;
c) x 2 x + 2 = 2 x x 2 − 2 x − 3 + x 6 − 2 x ;
d) 4 x 3 − x 2 − x + 1 − 3 1 − x 2 = 1 x + 1 .
Phương trình
x
+
1
x
−
1
2
x
−
1
x
−
1
có bao nhiêu nghiệm? A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Phương trình x + 1 x − 1 = 2 x − 1 x − 1 có bao nhiêu nghiệm?
A. 0
B. 1
C. 2
D. 3
Với điều kiện trên phương trình tương đương x 2 - x + 1 = 2 x - 1 ⇔ x = 1 hoặc x = 2
Đối chiếu điều kiện ta được phương trình có nghiệm duy nhất x = 2.
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
a) 1x−y1�−� + 2x+y2�+� + 3xy2−x23��2−�2 b) 1x−21�−2 + 1x+21�+2 - 4x−4x2−44�−4�2−4 c) x+1x+3�+1�+3 - x−13−x�−13−� + 2x−2x2x2−92�−2�2�2−9 d) 13x−213�−2 - 13x+213�+2 - 3x−64−9
Đọc tiếp
a) + + b) + - c) - + d) - -
a \(\dfrac{1}{x-y}+\dfrac{2}{x+y}+\dfrac{3x}{y^2-x^2}\)
\(=\dfrac{x+y+2x-2y-3x}{\left(x-y\right)\left(x+y\right)}=\dfrac{-y}{\left(x-y\right)\left(x+y\right)}\)
b: \(\dfrac{1}{x-2}+\dfrac{1}{x+2}-\dfrac{4x-4}{x^2-4}\)
\(=\dfrac{x+2+x-2-4x+4}{\left(x-2\right)\left(x+2\right)}=\dfrac{-2x+4}{\left(x-2\right)\left(x+2\right)}\)
=-2/x+2
c: \(\dfrac{x+1}{x+3}-\dfrac{x-1}{3-x}+\dfrac{2x-2x^2}{x^2-9}\)
\(=\dfrac{\left(x+1\right)\left(x-3\right)+\left(x-1\right)\left(x+3\right)+2x-2x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x^2-2x-3+x^2+2x-3+2x-2x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{2x-6}{\left(x+3\right)\left(x-3\right)}=\dfrac{2}{x+3}\)
Đúng 0
Bình luận (0)