Cho tam giác ABC.Tìm tập hợp điểm M sao cho /vecto MA+3MB-2MC/ =/2MA-MB-MC/

Những câu hỏi liên quan
Cho tam giác ABC có trọng tâm G, E là trung điểm của BC. Tập hợp các điểm M sao cho
2
M
A
→
+
M
B
→
+
M
C
→
...
Đọc tiếp
Cho tam giác ABC có trọng tâm G, E là trung điểm của BC. Tập hợp các điểm M sao cho 2 M A → + M B → + M C → = 3 M B → + M C →
A. Trung điểm của GE
B. Trung trực của GE
C. Trung trực của BC
D. Trọng tâm G
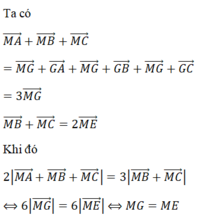
Suy ra tập họp các điểm M cần tìm là đường trung trực của đoạn GE.
Đáp án B
Đúng 0
Bình luận (0)
Cho tam giác ABC . Tìm tập hợp điểm M thỏa mãn :
a) |vecto MA+ vecto MC | = |vecto MA- vecto MB|
b) |2 vecto MA + vecto MB | = |4 vecto MB - vecto MC |
c) |4 vecto MA - vecto MB + vecto MC |=|2 vecto MA - vecto MB - vecto MC |
Cảm ơn trc , ai đó có thể giúp mình nhanh được không ạ , tại mình đang cần gấp :)))
MA+MC= MA-MB
<=> 2 MI=BA
=> MI=BA/2
=> I thuộc đường tròn I bán kính AB/2
Đúng 0
Bình luận (1)
nãy mk quên giải thik:
a, gọi I la trung điểm của AC=> MA+MC=2MI
hok tốt
Đúng 0
Bình luận (0)
b, 2MA+MB=4MB-MC
gọi I: 2OA+IB=0
gọi J: 4JB-JC=0
có:
3MI=3MJ
MI=MJ
=> M thuộc đường trung trục của IJ
Đúng 0
Bình luận (0)
Cho tam giác ABC
a) Xác định điểm D thỏa mãn vecto DA +3. vecto DB=0
b) Tìm tập hợp điểm M thỏa mãn: |MA+MB|=|MA+MC| câu b đều là vecto hết nha mn
Cho tam giac ABC. tim quy tich diem M sao cho | 2MA - MB | = | 2MC + MB | . CAI NAY LA VECTO NHA MN
Cho tam giác ABC. Tìm tập hợ điểm M sao cho
|vecto MA + vecto MB - vecto MC|= |2× vecto MA - vecto MB - vecto MC|
Giúp mình gấp nhé. Mai thi rồi
Cho tam giác ABC Xác định vị trí điểm M sao cho vecto MA - vecto MB + vecto MC = vecto 0
Ta thấy \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MA}+\overrightarrow{BM}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}=\overrightarrow{CM}\)
Như vậy, điểm M chính là đỉnh thứ tư của hình bình hành ABCM.
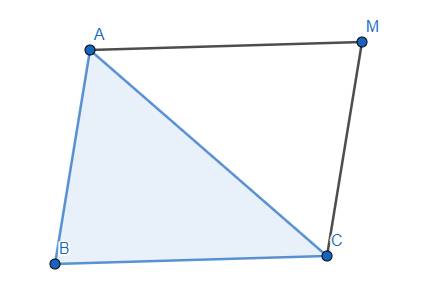
Đúng 1
Bình luận (0)
cho tam giác ABC
tìm điểm O sao cho : vecto OA+vecto OB+vecto OC= vecto 0
tìm điểm K sao cho : vecto KA+2 vecto KB= vecto CB
tìm điểm M sao cho : vecto MA+ vecto MB+ 2 vecto MC = vecto 0
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}\)⇒ O là trọng tâm tam giác ABC
\(\overrightarrow{K\text{A}}+2\overrightarrow{KB}=\overrightarrow{CB}=\overrightarrow{0}\Rightarrow\overrightarrow{K\text{A}}+\overrightarrow{KB}+\overrightarrow{KB}+\overrightarrow{BC}=\overrightarrow{0}\Rightarrow\overrightarrow{K\text{A}}+\overrightarrow{KB}+\overrightarrow{KC}=\overrightarrow{0}\)
⇒ K là trọng tâm tam giác ABC
Câu cuối chịu :))
Đúng 0
Bình luận (0)
cho tam giác ABC , tìm tập hợp điểm M thỏa mãn | 2 lần vecto MA+ 3 lần vecto MB|=|3 lần vecto MB+ 2 lần vecto MC|
Cho tam giác ABC. Tập hợp các điểm M sao cho
M
A
→
+
M
B
→
M
C
→
+
M...
Đọc tiếp
Cho tam giác ABC. Tập hợp các điểm M sao cho M A → + M B → = M C → + M B → | là:
A. Đường trung trực của BC
B. Đường tròn tâm I, bán kính R = 2AB với I nằm trên cạnh AB sao cho IA = 2IB
C. Đường trung trực của EF với E, F lần lượt là trung điểm của AB và BC
D. Đường tròn tâm I, bán kính R = 2AC với I nằm trên cạnh AB sao cho IA = 2IB
Gọi E và F lần lượt là trung điểm của AB; BC. Khi đó, ta có
M A → + M B → = M C → + M B → ⇔ 2 M E → = 2 M F → ⇔ M E → = M F →
Do đó, M thuộc đường trung trực của EF.
Đáp án C
Đúng 0
Bình luận (0)














