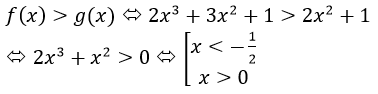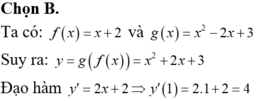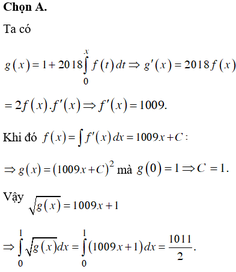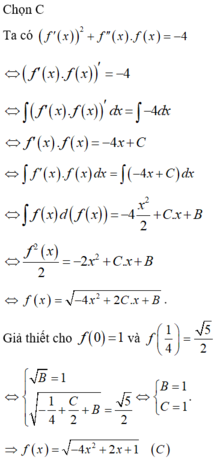d) Để (C) nằm phía trên (P) thì 2 hàm số f(x) và g(x) phải thõa mãn điều kiện sau:

Những câu hỏi liên quan
Cho hàm số liên tục trên khoảng (a;b) và
x
0
∈
(
a
;
b
)
.
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?(1) Hàm số đạt cực trị tại điểm
x
0
khi và chỉ khi
f
(
x
0
)
0
.
(2) Nếu hàm số
y
f
(
x
)
có đạo hàm và có đạo...
Đọc tiếp
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ ( a ; b ) . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' ( x 0 ) = 0 .
(2) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = f ' ' ( x 0 ) = 0 thì điểm x 0 không phải là điểm cực trị của hàm số y = f ( x ) .
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
(4) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = 0 , f ' ' ( x 0 ) > 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
A. 1
B. 2
C. 0
D. 3
Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
Đúng 0
Bình luận (0)
Cho hàm số f(x) liên tục và có đạo hàm trên
R
1
3
thỏa mãn các điều kiện sau:
f
(
x
)
(
3
x
+
2
)
+
f
(
x
)
(
3
x
-
1
)
x
2
+
1
;
f
(
0
)...
Đọc tiếp
Cho hàm số f(x) liên tục và có đạo hàm trên R \ 1 3 thỏa mãn các điều kiện sau: f ( x ) ( 3 x + 2 ) + f ' ( x ) ( 3 x - 1 ) = x 2 + 1 ; f ( 0 ) = - 3 Khi đó giá trị của ∫ 1 2 f ( x ) d x nằm trong khoảng nào dưới đây?
A. (0;1)
B. (1;2)
C. (3;4)
D. (2;3)
Cho hàm số yf(x)0 xác định và có đạo hàm trên đoạn [0;1] và thỏa mãn các điều kiện sau: g(x)1+2018
∫
0
x
f
(
t
)
dt
;
g
(
x
)
f
2
(...
Đọc tiếp
Cho hàm số y=f(x)>0 xác định và có đạo hàm trên đoạn [0;1] và thỏa mãn các điều kiện sau: g(x)=1+2018 ∫ 0 x f ( t ) dt ; g ( x ) = f 2 ( x ) . Tính ∫ 0 1 ( g ( x ) dx ?
A. 1011/2.
B. 1009/2.
C. 2019/2.
D. 505
Cho hàm số y = f(x) = mx + 2m − 3 có đồ thị (d). gọi A, B là hai điểm thuộc đồ thị
và có hoành độ lần lượt là −1 và 2.
1 Xác định tọa độ hai điểm A và B.
2 Tìm m để cả hai điểm A và B cùng nằm phía trên trục hoành.
3 Tìm điều kiện của m để f(x) > 0, ∀x ∈ [−1; 2]
TRÊN TIA AB LẤY HAI ĐIỂM E VÀ F SAO CHO AE=4CM , AF = 7CM
a) tính EF
b) gọi G là trung điểm của EF , tính AG
c) độ dài ab phải thỏa mãn điều kiện gì để các điểm E ,G,F nằm về một phía của B ?
A----------------------------E-----/----G----/-----F------------------------
a) AE <AF => E nằm giữa A;F => AE +EF =AF => EF = AF -AE = 7 -4 = 3 cm
b) G là trung điểm EF => EG = EF/2
AG = AE + EG = AE + EF/2 =4 +3/2 = 5,5 cm
c) Để E,G,F cùng nằm 1 phía của B nếu : + AB >ÀF hay AB > 7 cm
hoặc AB< AE hay AB <4 cm
Đúng 0
Bình luận (0)
Cho hàm số y=f(x) xác định và liên tục trên R thõa mãn các điều kiện sau:
\(\hept{\begin{cases}f\left(x\right)>0,\forall x\in R\\f'\left(x\right)=-e^xf^2\left(x\right),\forall x\in R\\f\left(o\right)=\frac{1}{2}\end{cases}}\)
Hãy tính \(f\left(ln2\right)\).
Cho hàm số y f(x) có đồ thị (C) nằm trên trục hoành. Hàm số y f(x) thỏa mãn các điều kiện
y
2
+
y
.
y
-
4
và
f
0
1
;
f...
Đọc tiếp
Cho hàm số y = f(x) có đồ thị (C) nằm trên trục hoành. Hàm số y = f(x) thỏa mãn các điều kiện y ' 2 + y ' ' . y = - 4 và f 0 = 1 ; f 1 4 = 5 2 Diện tích hình phẳng giới hạn bởi (C) và trục hoành gần nhất với số nào dưới đây?
A. 0,95.
B. 0,96.
C. 0,98.
D. 0,97.
Cho hàm số liên tục trên khoảng (a;b) và
x
0
∈
a
;
b
. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau ?(1) Hàm số đạt cực trị tại điểm
x
0
khi và chỉ khi
f
x
0
0
(2) Nếu hàm số...
Đọc tiếp
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ a ; b . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau ?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' x 0 = 0
(2) Nếu hàm số y = f(x) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' x 0 = f " x 0 = 0 thì điểm x 0 không là điểm cực trị của hàm số y = f x
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f(x)
(4) Nếu hàm số y = f(x) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' x 0 = 0 , f " x 0 > 0 thì điểm x 0 là điểm cực đại của hàm số y = f(x)
A. 1
B. 2
C. 0
D. 3
Cho hàm số yf(x) liên tục và có đạo hàm trên R. Biết hàm số f’(x) có đồ thị được cho trong hình vẽ. Tìm điều kiện của m để hàm số g(x)f(2019)x – mx +2 đồng biến trên [0;1]
Đọc tiếp
Cho hàm số y=f(x) liên tục và có đạo hàm trên R. Biết hàm số f’(x) có đồ thị được cho trong hình vẽ. Tìm điều kiện của m để hàm số g(x)=f(2019)x – mx +2 đồng biến trên [0;1]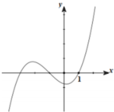
![]()
![]()
![]()
![]()