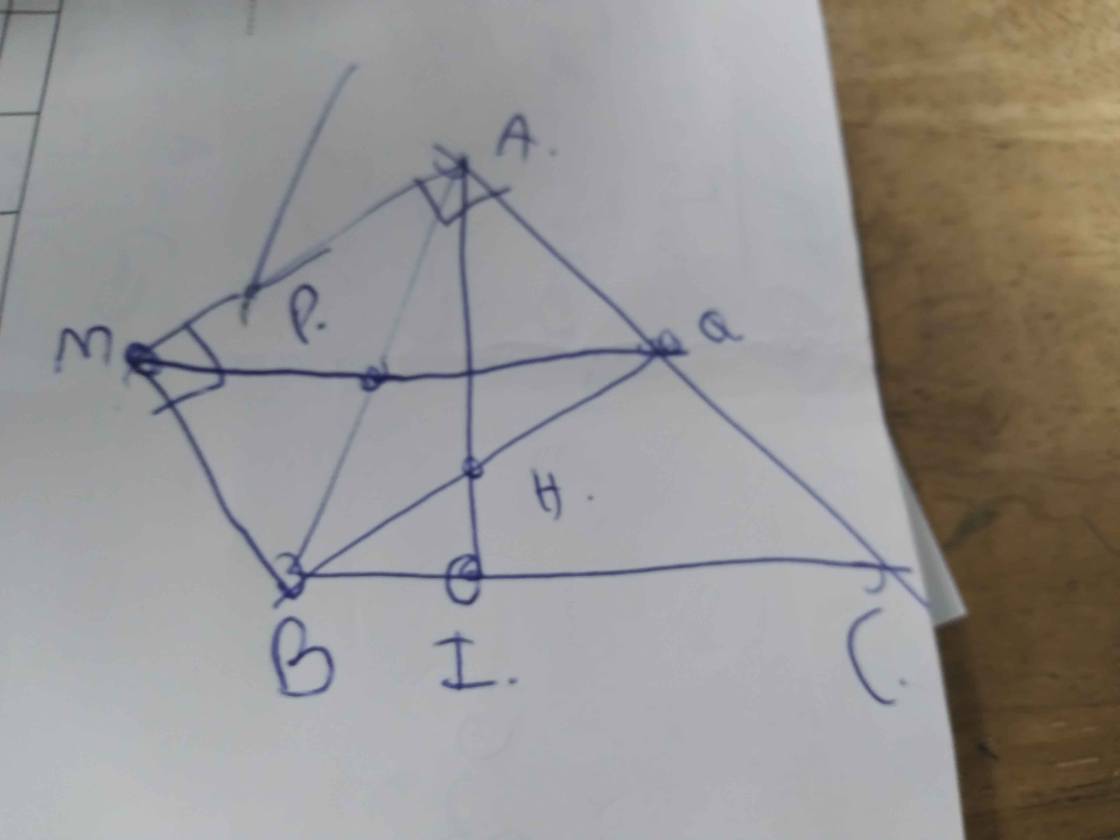
cho tam giac ABC có dường cao AI từ A kẻ tia Ax vuông góc với AC, BI song song AC, gọi M là giao điểm Ax và BI nối M với trung diểm của P của AB, đường MP cắt AC tại Q, PQ cắt AI tại H
Làm nhanh mih tích nha các bn vẽ cả hình nữa mih cho mih nha.

Những câu hỏi liên quan
cho tam giac ABC có dường cao AI từ A kẻ tia Ax vuông góc với AC, BI song song AC, gọi M là giao điểm Ax và BI nối M với trung diểm của P của AB, đường MP cắt AC tại Q, PQ cắt AI tại H
Cảm ơn OLM đã trừ điểm https://olm.vn/thanhvien/kimmai123az, e rất ghi nhận sự tiến bộ về sự công bằng của olm.Nhưng vẫn còn nhìu cây mà con chó này copy nek, mong olm xét ạ https://olm.vn/hoi-dap/detail/228356929591.html////////https://olm.vn/hoi-dap/detail/228472453946.html/////https://olm.vn/hoi-dap/detail/228437567447.html//////////https://olm.vn/hoi-dap/detail/228435268921.html
Vô trangh cá nhân của e sẽ thấy đc những câu trả lời "siêu hay" của con chóhttps://olm.vn/thanhvien/kimmai123az
Đúng 0
Bình luận (0)
Ko, mk nói con Mệt mỏi, link nó nek: https://olm.vn/thanhvien/kimmai123az
Đúng 0
Bình luận (0)
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
a) Tứ giác AMBQ là hình gì?
b) Chứng minh rằng CH AB ⊥ .
c) Chứng minh tam giác PIQ cân.
a: Xét ΔPMB và ΔPQA có
\(\widehat{PBM}=\widehat{PAQ}\)
PB=PA
\(\widehat{MPB}=\widehat{QPA}\)
Do đó: ΔPMB=ΔPQA
Suy ra: MB=AQ
Xét tứ giác AMBQ có
MB//AQ
MB=AQ
Do đó: AMBQ là hình bình hành
mà \(\widehat{MAQ}=90^0\)
nên AMBQ là hình chữ nhật
Đúng 4
Bình luận (0)
Câu a có r mk ko ghi lại nx nhe
b) Ta có AQBM là HCN (CMa)
=> ^AQB=900 hay BQ ⊥ AC
=> BQ là đường cao của ΔABC
Mà H là giao điểm của 2 đường cao AI và BQ của ΔABC (gt)
=> H là trực tâm của ΔABC
=> CH cũng là đường cao của ΔABC (H là trực tâm; H ∈ CH)
=> CH ⊥ AB (đpcm)
Đúng 1
Bình luận (0)
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
a) Tứ giác AMBQ là hình gì?
b) Chứng minh rằng CH⊥ AB .
c) Chứng minh tam giác PIQ cân.
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
a) Tứ giác AMBQ là hình gì?
c) Chứng minh tam giác PIQ cân.
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
a) Tứ giác AMBQ là hình gì?
b) Chứng minh rằng CH⊥ AB .
c) Chứng minh tam giác PIQ cân.
Mình đang cần rất2 cần phần C cứu mình
a: Xét ΔPMB và ΔPQA có
\(\widehat{PBM}=\widehat{PAQ}\)(hai góc so le trong, BM//AC)
PB=PA
\(\widehat{MPB}=\widehat{QPA}\)(hai góc đối đỉnh)
Do đó: ΔPMB=ΔPQA
=>PM=PQ
=>P là trung điểm của MQ
Xét tứ giác AMBQ có
P là trung điểm chung của AB và MQ
=>AMBQ là hình bình hành
Hình bình hành AMBQ có \(\widehat{MAQ}=90^0\)
nên AMBQ là hình chữ nhật
b: Ta có: AMBQ là hình chữ nhật
=>BQ\(\perp\)AQ tại Q
=>BQ\(\perp\)AC tại Q
Xét ΔABC có
BQ,AI là các đường cao
BQ cắt AI tại H
Do đó: H là trực tâm của ΔABC
=>CH\(\perp\)AB
c: Ta có: AMBQ là hình chữ nhật
=>AB=QM
mà \(PQ=\dfrac{QM}{2}\)
nên \(PQ=\dfrac{AB}{2}=PA\)(1)
Ta có: ΔAIB vuông tại I
mà IP là đường trung tuyến
nên IP=PA(2)
Từ (1) và (2) suy ra PI=PQ
=>ΔPIQ cân tại P
Đúng 0
Bình luận (0)
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
A) chứng minh tứ giác AQHM là hình thang
a: Xét ΔPBM và ΔPAQ có
\(\widehat{PBM}=\widehat{PAC}\)
PB=PA
\(\widehat{BPM}=\widehat{APQ}\)
Do đó: ΔPBM=ΔPAQ
=>PM=PQ
Xét tứ giác AQBM có
P là trung điểm chung của AB và QM
=>AQBM là hình bình hành
=>BQ//AM
=>HQ//AM
=>AQHM là hình thang
Đúng 1
Bình luận (0)
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
a) chứng minh tứ giác AQHM là hình thang
b) tứ giác AMBQ là hình gì ? vì sao?
a: Xét ΔPMB và ΔPQA có
\(\widehat{PBM}=\widehat{PAQ}\)
PB=PA
\(\widehat{MPB}=\widehat{QPA}\)
Do đó: ΔPMB=ΔPQA
=>PM=PQ
Xét ΔPBQ và ΔPAM có
PB=PA
\(\widehat{BPQ}=\widehat{APM}\)
PQ=PM
Do đó: ΔPBQ=ΔPAM
=>\(\widehat{PBQ}=\widehat{PAM}\)
mà hai góc này là hai góc so le trong
nên BQ//AM
=>HQ//AM
=>AQHM là hình thang
b: Xét tứ giác AMBQ có
AQ//BM
BQ//AM
Do đó: AMBQ là hình bình hành
Đúng 2
Bình luận (0)
Bài 3/ Cho tam giác ABC nhọn, có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.a) Chứng minh tứ giác AQHM là hình thang.b) Tứ giác AMBQ là hình gì? Vì sao?c) Chứng minh tam giác PIQ cân.em xin lời giải chi tiết ạ
Đọc tiếp
Bài 3/ Cho tam giác ABC nhọn, có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
a) Chứng minh tứ giác AQHM là hình thang.
b) Tứ giác AMBQ là hình gì? Vì sao?
c) Chứng minh tam giác PIQ cân.
em xin lời giải chi tiết ạ
a,b: Xét ΔPMB và ΔPQA có
\(\widehat{PBM}=\widehat{PAQ}\)
PB=PA
\(\widehat{MPB}=\widehat{QPA}\)
Do đó: ΔPMB=ΔPQA
=>PM=PQ
=>P là trung điểm của MQ
Xét tứ giác AQBM có
P là trung điểm chung của AB và QM
=>AQBM là hình bình hành
=>AM//BQ
=>BQ\(\perp\)AC
Xét tứ giác AQHM có HQ//AM
nên AQHM là hình thang
Đúng 4
Bình luận (0)