Gọi E, F là trung điểm AB, CD của hình bình hành ABCD
a) CMR: AF // CE
b) CMR: AF và CE chia đường chéo BD thành 3 phần bằng nhau.
HELP ME T^T
Gọi E, F lần lươt là trung điểm của AB và CD của hình bình hành ABCD. Chứng minh
a) AF// CE
b) Chứng minh AF và CE chia đường chéo BD thành 3 phần bằng nhau.
Gọi E, F là trung điểm AB, CD của hình bình hành ABCD
a) CMR: AF // CE
b) CMR: AF và CE chia đường chéo BD thành phần bằng nhau.
HELP ME T^T
xét tam giác ADF và tam giác CBE có
AD=BC ( 2 cạnh bên của HBH ABCD )
EB=DF ( E là trung điểm của AB , F là trung điểm của DC )
góc ADF= goc CBE
=> tam giác ADF= tam giác CBE ( c_g_c)
-> AF=CE ( cặp cạnh tương ứng)
AECF là hình bình hành vì
AE=CF (gt)
AF=EC (cmt)
=>AECF là hình bình hành
-> AF song song CE
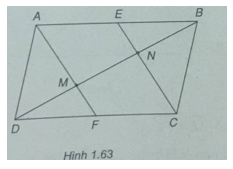
Cho hình bình hành ABCD. Gọi E, F thứ tự là trung điểm của AB và CD. M là giao điểm của AF và DE, N là giao điểm của BF và CE.
a) CMR: Tứ giác EMFN là hình bình hành
b) CMR: AC, EF, MN đồng quy
c) Gọi I, K lần lượt là giao điểm của AF và CE với BD. CMR: BK=KI=ID
Cho hình bình hành ABCD. Gọi O là giao điểm của 2 đường chéo AC và BD. M và N lần lượt là trung điểm của OD và OB. Gọi E là giao điểm của AM và CD. F là giao điêm của CN và AB. CMR:
a) Tứ giác AMCN là hình bình hành
b) AF= CE
c) DE= 1/2EC
Cho hình bình hành ABCD, có AB = 2AD gọi E, F theo thứ tự là trung điểm của AB và CD.
a, CMR: AECF là hình bình hành
b, CMR: AEFD là hình thoi
c, AF cắt DE tại R, CE cắt BF tại S. CM: ERFS là hình chữ nhật
d, Gọi I và K lần lượt là giao điểm của BD với AF và BD với CE. CM: tam giác EIK cân.
Bài 1 :Cho hình bình hành ABCD. E,F thứ tự là trung điểm của AB và CD.
a, AF song song CD
b, M,N thứ tự là giao điểm của BD vs AF, CE
Bài 2: Cho hình bình hành ABCD. Trên đg chéo BD lấy E,F sao cho DE =BF.CMR: AF song song CE
Bài 1:
Kẻ đường chéo AC
có E,F,G,H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA
suy ra EF là đường trung bình của tam giác ABC nên EF//=1/2AC (1)
GH là đường trung bình của tam giác ADC nên GH//=1/2AC (2)
Từ (1) và (2) suy ra EF//=GH nên EFGH là hình bình hành
Vì có hai cạnh đối song song và bằng nhau
Bài 1
a)Ta có:AE=AB/2=AD=CD/2=DF
Tứ giác AEFD có: AE//DF, AE=DF
AEFD là hbh
mà AE=AD nên AEFD là hình thoi
CMTT ta có: BEFC là hình thoi
Ta có: AE=AB/2=AD=BC=CD/2=CF
Tứ giác AECF có: AE//CF, AE=CF
AECF là hbh
b)Ta có: AEFD là hình thoi nên: góc AED=FED
mà : AED=DEF
FED=EDC
CMTT ta có:FEC=ECD
Mà FED+DEC+FEC+ECD=180
2ˆFED+2ˆFEC=180o2FED^+2FEC^=180o
2DEC=180.2DEC=180
DEC=90o
Tứ giác EMFN có: EM//FN, EN//FM và EMFN là hbh
mà MEN=90o nên EMFN là hcn
Cho hình bình hành ABCD, các đường chéo cắt nhau tại O. Gọi E, F theo thứ tự là trung điểm của OD, OB. K là giao điểm của AE và CD. CMR:
a, AF//CE
b, DK=1/2 KC
Bài này dễ lắm lun
cho hình bình hành ABCD gọi E,F theo thứ tự là trung điểm của AB,CD Gọi M là giao điểm của AF và DE, N là giao điểm BF và CE
a) CMR EMFN là hình bình hành
b) Các Đường thẳng AC, EF, MN Đồng quy
Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của AB và CD. Nối AF và CE, 2 đường này cắt đường chéo BD lần lượt tại M và N. Chứng minh vectơ DM = vectơ MN = vectơ NB.
AECF là hình bình hành => EN // AM
E là trung điểm của AB => N là trung điểm của BM, do đó MN = NB.
Tương tự, M là trung điểm của DN, do đó DM = MN.
Vậy →DM=→MN=→NB