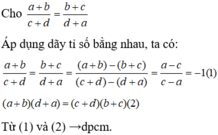chứng tỏ rằng: nếu a + b/ c + d = b + c/ d + a (trong đó a + b + c + d khác 0) thì a = c

Những câu hỏi liên quan
Chứng tỏ rằng: Nếu (a+b)/(c+d)=(b+c)/(b+a)(trong đó a+b+c+d khác 0)) thì a = c.
Chứng tỏ rằng: Nếu
a
+
b
c
+
d
b
+
c
d
+
a
(trong đó
a
+
b
+
c
+
d
≠
0
) thì
a
c
.
Đọc tiếp
Chứng tỏ rằng: Nếu a + b c + d = b + c d + a (trong đó a + b + c + d ≠ 0 ) thì a = c .
chứng minh rằng ,nếu \(\frac{a+b}{c+a}=\frac{b+c}{d+a}\)trong đó a,b,c,d khác 0 thì a=c
Chứng minh rằng nếu a+b/b+c =c+d/d+a (c+d khác 0) thì a=c và a+b+c+d=0
a) Chứng tỏ rằng nếu a/b < c/d (b>0,d>0) thì a/b < a+c/b+d < c/d
\(\frac{a}{b}< \frac{c}{d}\rightarrow ad< bc\)
\(\rightarrow ad+ab< bc+ab\)
\(\rightarrow a.\left(b+d\right)< b.\left(a+c\right)\)
\(\rightarrow\frac{a}{b}< \frac{a+c}{b+d}\) \(\left(1\right)\)
\(\text{Ta có:}\)
\(ad< bc\)
\(\rightarrow ad+cd< bc+cd\)
\(\rightarrow d.\left(a+c\right)< c.(b+d)\)
\(\rightarrow\frac{a+c}{b+d}< \frac{c}{d}\) \(\left(2\right)\)
\(\text{Từ}\)\(\left(1\right)\)\(\text{và}\)\(\left(2\right)\)\(\rightarrow\)\(\frac{a}{b}< \frac{a+c}{b+d}< \frac{c}{d}\)
chứng tỏ rằng nếu a\b <c\d (b>0,d>0) thì a\b < a+c\b+d < c\d
chứng tỏ rằng nếu a/b<c/d (b>0/d>0) thì a/b < a+c/b+d<c/d
* a/b < c/d => ad < cb
=>ad +ab < bc+ab
=> a(d+b) < b(a+c)
=> a/b < a+c/d+b (1)
* a/b < c/d => ad<cb
=> ad + cd < cb +cd
=> d(a+c) < c(b+d)
=> c/d > a+c/b+d (2)
Từ (1) và (2) => a/b < a+c/b+d < c/d
Đúng 0
Bình luận (0)
chứng tỏ rằng nếu a/b < c/d ( b>0,d>0) thì a/b < a+c/b+d<c/d
Ta có : \(\frac{a}{b}< \frac{c}{d}\Rightarrow ad< bc\)
\(\Rightarrow ab+ad< ab+bc\)
\(\Rightarrow a.\left(b+d\right)< b.\left(a+c\right)\)
\(\Rightarrow\frac{a}{b}< \frac{a+c}{b+d}\left(1\right)\)
Ta lại có : \(ad< bc\Rightarrow ad+cd< bc+cd\)
\(\Rightarrow d.\left(a+c\right)< c.\left(b+d\right)\)
\(\Rightarrow\frac{a+c}{b+d}< \frac{c}{d}\left(2\right)\)
Từ (1) và (2), suy ra nếu :\(\frac{a}{b}< \frac{c}{d}\)
thì : \(\frac{a}{b}< \frac{a+c}{b+d}< \frac{c}{d}\)
Đúng 0
Bình luận (0)
chứng tỏ rằng nếu a/b < c/d (b>0/d>0) thì a/b < a+c/b+d <c/d