Thu gọn biểu thức .
A=\(\frac{1}{2-\sqrt{3}}+\frac{1}{2+\sqrt{5}}\)
Những câu hỏi liên quan
A=\(\sqrt{45a}-2\sqrt{\frac{4a}{3}}+\frac{\sqrt{18a}}{\sqrt{6}}+\sqrt{5\frac{1}{3}a}\)
Rút gọn biểu thức A
Rút gọn biểu thức sau
\(A=\frac{\sqrt{x+2}}{\sqrt{x-3}}-\frac{\sqrt{x+1}}{\sqrt{x-2}}-\frac{3\sqrt{x-3}}{x-5\sqrt{x+6}}\)
Rút gọn biểu thức sau
\(A=\frac{\sqrt{x-3}}{\sqrt{x-2}}-\frac{2\sqrt{x-1}}{\sqrt{x-1}}+\frac{x-2}{x-2\sqrt{x+}2}\)
Cho biểu thức:
\(\frac{a}{\sqrt{a^2-b^2}}-(1+\frac{a}{\sqrt{a^2-b^2}})\div\frac{b}{a-\sqrt{a^2-b^2}}\)
với a>b>0
a, Rút gọn biểu thức
b, Xác định giá trị của biểu thức khi a bằng 3b
Đặt \(A=\frac{a}{\sqrt{a^2-b^2}}-\left(1+\frac{a}{\sqrt{a^2-b^2}}\right):\frac{b}{a-\sqrt{a^2-b^2}}\)
\(A=\frac{a}{\sqrt{a^2-b^2}}-\frac{\left(a+\sqrt{a^2-b^2}\right)\left(a-\sqrt{a^2-b^2}\right)}{b\sqrt{a^2-b^2}}\)
\(A=\frac{a}{\sqrt{a^2-b^2}}-\frac{a^2-a^2+b^2}{b\sqrt{a^2-b^2}}\)
\(A=\frac{a}{\sqrt{a^2-b^2}}-\frac{b}{\sqrt{a^2-b^2}}\)
\(A=\frac{a-b}{\sqrt{a-b}.\sqrt{a+b}}\)
\(A=\frac{\sqrt{a-b}}{\sqrt{a+b}}\)
Với \(a=3b\) ta có : \(A=\frac{\sqrt{a-b}}{\sqrt{a+b}}=\frac{\sqrt{3b-b}}{\sqrt{3b+b}}=\frac{\sqrt{2b}}{\sqrt{4b}}=\frac{\sqrt{2}}{2}\)
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
\(\frac{a}{\sqrt{a^2-b^2}}-\left(1+\frac{a}{\sqrt{a^2-b^2}}\right):\frac{b}{a-\sqrt{a^2-b^2}}\)
\(=\frac{a}{\sqrt{a^2-b^2}}-\frac{a+\sqrt{a^2-b^2}}{\sqrt{a^2-b^2}}.\frac{a-\sqrt{a^2-b^2}}{b}\)
\(=\frac{a}{\sqrt{a^2-b^2}}-\frac{a^2-a^2+b^2}{\sqrt{a^2-b^2}b}\)
\(=\frac{ab-a^2+a^2-b^2}{\sqrt{a^2-b^2}b}\)
\(=\frac{b\left(a-b\right)}{\sqrt{\left(a-b\right)\left(a+b\right)}b}\)
\(=\frac{\sqrt{a-b}}{\sqrt{a+b}}\)
b, Thay a = 3b
\(=\sqrt{\frac{3b-b}{3b+b}}=\sqrt{\frac{2}{4}}=\sqrt{\frac{1}{2}}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho \(A=\frac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\frac{\sqrt{x}+3}{\sqrt{x}-2}-\frac{2\sqrt{x}+1}{3-\sqrt{x}}\)
Rút gọn biểu thức A
Làm giúp mik vứi mấy bn ui
đúng mik tick
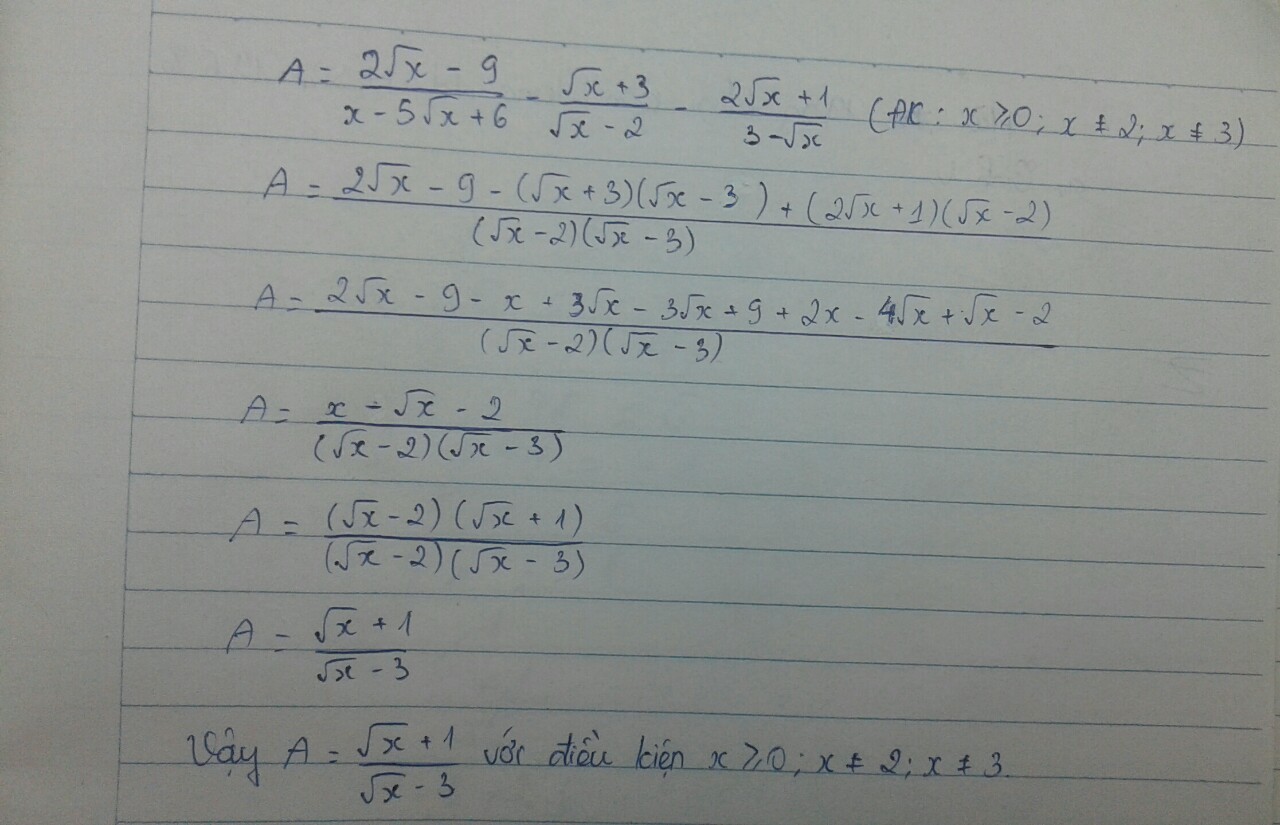mình trình bày trong hình, hơi mờ bạn thông cảm!
như này là xịn lém rrr. Thănkiu nhìu nhó Nguyen Thu Hong
1.cho biểu thức Pleft(frac{2x+sqrt{x}}{xsqrt{x}-1}-frac{2}{x+sqrt{x}+1}+frac{1}{1-sqrt{x}}right):frac{sqrt{x}-1}{2}a, rút gọn biểu thức Pb,tìm các giá trị của x để biểu thức P có giá trị nguyên2.. tìm các cặp số nguyên(x;y) thỏa mãn x^2+xy-3x-y-503..giải phương trình 2sqrt{2x+4}+4sqrt{2-x}sqrt{9x^2+16}
Đọc tiếp
1.cho biểu thức \(P=\left(\frac{2x+\sqrt{x}}{x\sqrt{x}-1}-\frac{2}{x+\sqrt{x}+1}+\frac{1}{1-\sqrt{x}}\right):\frac{\sqrt{x}-1}{2}\)
a, rút gọn biểu thức P
b,tìm các giá trị của x để biểu thức P có giá trị nguyên
2.. tìm các cặp số nguyên(x;y) thỏa mãn \(x^2+xy-3x-y-5=0\)
3..giải phương trình \(2\sqrt{2x+4}+4\sqrt{2-x}=\sqrt{9x^2+16}\)
câu 1 : Giải pt sau a . 2x-2sqrt{2x}-10câu 2 : thu gọn các biểu thức sau Afrac{3+sqrt{5}}{3-sqrt{5}}+frac{3-sqrt{5}}{3+sqrt{5}}Bsqrt{12-6sqrt{3}}+sqrt{21-12sqrt{3}}C5left(sqrt{2+sqrt{3}}+sqrt{3-sqrt{5}}-sqrt{frac{5}{2}}right)^2+left(sqrt{2-sqrt{3}}+sqrt{3+sqrt{5}}-sqrt{frac{3}{x}}right)^2
Đọc tiếp
câu 1 : Giải pt sau
a . \(2x-2\sqrt{2x}-1=0\)
câu 2 : thu gọn các biểu thức sau
\(A=\frac{3+\sqrt{5}}{3-\sqrt{5}}+\frac{3-\sqrt{5}}{3+\sqrt{5}}\)
\(B=\sqrt{12-6\sqrt{3}}+\sqrt{21-12\sqrt{3}}\)
\(C=5\left(\sqrt{2+\sqrt{3}}+\sqrt{3-\sqrt{5}}-\sqrt{\frac{5}{2}}\right)^2+\left(\sqrt{2-\sqrt{3}}+\sqrt{3+\sqrt{5}}-\sqrt{\frac{3}{x}}\right)^2\)
1) ĐK:x\(\ge\frac{1}{2}\)
PT\(\Leftrightarrow\sqrt{2x-1}=x\)
\(\Leftrightarrow\begin{cases}x\ge0\\2x-1=x^2\end{cases}\)
\(\Leftrightarrow\begin{cases}x\ge0\\x=1\end{cases}\)
\(\Leftrightarrow x=1\) (thỏa mãn)
Đúng 0
Bình luận (0)
\(A=\frac{\left(3+\sqrt{5}\right)^2+\left(3-\sqrt{5}\right)^2}{\left(3+\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(A=\frac{18+10}{4}\)
\(A=7\)
Đúng 0
Bình luận (0)
\(B=\sqrt{9-3\times2\sqrt{3}+3}+\sqrt{12-2\times3\times2\sqrt{3}+9}\)
\(B=\sqrt{\left(3-\sqrt{3}\right)^2}+\sqrt{\left(2\sqrt{3}-3\right)^3}\)
\(B=\left|3-\sqrt{3}\right|+\left|2\sqrt{3}-3\right|\)
\(B=3-\sqrt{3}+2\sqrt{3}-3\)
\(B=\sqrt{3}\)
Đúng 0
Bình luận (0)
Cho biểu thức : A=\(\frac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\frac{\sqrt{x}+3}{\sqrt{x}-2}-\frac{2\sqrt{x}+1}{3-\sqrt{x}}\)
a, Rút gọn A
b,Tìm các giá trị của x để A <1
c,Tìm các giá trị nguyên của x sao cho A nguyên
Rút gọn biểu thức :
a , \(\sqrt{\frac{x-2\sqrt{x}+1}{x+2\sqrt{x}+1}}\) ( x > hoặc = 0 )
