Tìm GTNN của A = (x-y)2 + 6y(x-y) +x2+16y2-8xy+2x-8y+10 (x,y,a thuộc Z )
Những câu hỏi liên quan
Câu 1: Kết quả của phép nhân (x-4)(x+5) bằngA.X-x-20 B. x +x+20 С. x? +х - 20 D. x2 +x+1Câu 2: Biểu thức x² - 8xy+16y2 viết dưới dạng hằng đằng thức làD. (x-16y) A. (4y-x)B. (x-8y)C. (x+4y)?Câu 3. Kết quả của phép chia xy 2 xy* bằngA. 2xyB. ½ xyС. 2хDxB/ Tự luận Bài 1. Tính al (x-3x+2) (x-1) b/ ( 4x*y2 – 6x²y? + 2x³y?): 2x²y?Bài 2. Tìm x biết al (x-2) - x(x+1) 5Bài 4. Cho tam giác ABC vuông tại A có trung tuyên AM. Vẽ D đôi xứng với A qua M. tứ giác ABDC là hình gì? Vì sao?
Đọc tiếp
Câu 1: Kết quả của phép nhân (x-4)(x+5) bằng
A.X-x-20 B. x +x+20 С. x? +х - 20 D. x2 +x+1
Câu 2: Biểu thức x² - 8xy+16y2 viết dưới dạng hằng đằng thức là
D. (x-16y) A. (4y-x)
B. (x-8y)
C. (x+4y)?
Câu 3. Kết quả của phép chia x'y 2 x'y* bằng
A. 2xy
B. ½ xy
С. 2х
Dx
B/ Tự luận Bài 1. Tính al (x-3x+2) (x-1) b/ ( 4x*y2 – 6x²y? + 2x³y?): 2x²y?
Bài 2. Tìm x biết al (x-2) - x(x+1) = 5
Bài 4. Cho tam giác ABC vuông tại A có trung tuyên AM. Vẽ D đôi xứng với A qua M. tứ giác ABDC là hình gì? Vì sao?
Câu 1: Kết quả của phép nhân (x-4)(x+5) bằng A.X-x-20 B. x +x+20 С. x? +х - 20 D. x2 +x+1 Câu 2: Biểu thức x² - 8xy+16y2 viết dưới dạng hằng đằng thức là D. (x-16y) A. (4y-x) B. (x-8y) C. (x+4y)? Câu 3. Kết quả của phép chia xy 2 xy* bằng A. 2xy B. ½ xy С. 2х Dx B/ Tự luận Bài 1. Tính al (x-3x+2) (x-1) b/ ( 4x*y2 – 6x²y? + 2x³y?): 2x²y? Bài 2. Tìm x biết al (x-2) - x(x+1) 5 Bà 4. Cho tam giác ABC vuông tại A có trung tuyên AM. Vẽ D đôi xứng với A qua M. tứ giác ABDC là hình gì? Vì sao?
Đọc tiếp
Câu 1: Kết quả của phép nhân (x-4)(x+5) bằng A.X-x-20 B. x +x+20 С. x? +х - 20 D. x2 +x+1 Câu 2: Biểu thức x² - 8xy+16y2 viết dưới dạng hằng đằng thức là D. (x-16y) A. (4y-x) B. (x-8y) C. (x+4y)? Câu 3. Kết quả của phép chia x'y 2 x'y* bằng A. 2xy B. ½ xy С. 2х Dx B/ Tự luận Bài 1. Tính al (x-3x+2) (x-1) b/ ( 4x*y2 – 6x²y? + 2x³y?): 2x²y? Bài 2. Tìm x biết al (x-2) - x(x+1) = 5 Bà 4. Cho tam giác ABC vuông tại A có trung tuyên AM. Vẽ D đôi xứng với A qua M. tứ giác ABDC là hình gì? Vì sao?
phân tích đa thức thành nhân tử 1, A = 2x^2 + 5x^3 + x^2y 2, A = 4x^2y - 8xy^2 + 18x^2y^2 3, A = -3x^2y + 6x^2 y^2 4, A = 2x^3 y^4 - 4x^5 y^6 + 6y^7 x^8 5, A = 14x^2y - 21xy^2 + 28x^2 y^2 6, A = -8x^4 y^3 - 12x^2 y^4 + 20x^3 y^4 7, A = 5x . (x - 1) - 15x . (1 - x) 8, A = 2x^2 . (y - 1) - 15x . (1 - x) 9, A = 9x^2 . (y + z ) + 3x . (y + z) 10, A = 10x . ( x - y) - 8y . (y - x) 11, A = 2x . ( x + y) - 6x^2 . (x + y) 12, A = 10xy . ( x - y) - 6y . (y - x) giải giúp e với ạ
Xem chi tiết
Tìm tâm và bán kính của các đường tròn sau:
a, x2 + y2– 2x – 2y - 2 = 0
b, 16x2 + 16y2 + 16x – 8y -11 = 0
c, x2 + y2 - 4x + 6y – 3 = 0
Cách 1 : Xác định các hệ số a, b, c.
a) x2 + y2 – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2
⇒ tâm I (1; 1) và bán kính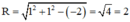 
b) 16x2 + 16y2 + 16x – 8y –11 = 0
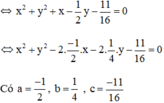
⇒ Đường tròn có tâm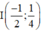 
, bán kính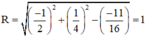 
c) x2 + y2 - 4x + 6y - 3 = 0
⇔ x2 + y2 - 2.2x - 2.(-3).y - 3 = 0
có hệ số a = 2, b = -3,c = -3
⇒ Đường tròn có tâm I(2 ; –3), bán kính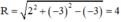 
Cách 2 : Đưa về phương trình chính tắc :
a) x2 + y2 - 2x - 2y - 2 = 0
⇔ (x2 - 2x + 1) + (y2 - 2y +1) = 4
⇔(x-1)2 + (y-1)2 = 4
Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.
b) 16x2 + 16y2 + 16x - 8y - 11 = 0
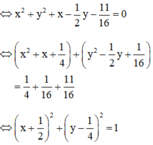
Vậy đường tròn có tâm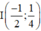 
và bán kính R = 1.
c) x2 + y2 - 4x + 6y -3 = 0
⇔ (x2 - 4x + 4) + (y2 + 6y + 9) = 4 + 9 + 3
⇔ (x - 2)2 + (y + 3)2 = 16
Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.
Đúng 0
Bình luận (0)
TIM GTNN :
B= 5x^2 -x-2
C=x^ -4xy +7y^2+y+5
D = x^2 +y^2+z^2-xy-yz-zx-+5
E = x^2- 2xy -4x+2y^2+6y+10
F = 4x^2 +4xy+4x+3y^2+8y+20
H = (x^2-2x+3)*(x^2-2x+5)+10
2x^2+xy+2y^2 = 5/4.(x+y)^2 + 3/4. (x-y)^2 >= 5/4. (x+y)^2
=> cbh(2x^2+xy+2y^2) >= cbh5 / 2. (x+y)
tương tự với 2 căn còn lại.. cộng vế ta có VT >= cbh5 ( x+y+z) = cbh5 : dpcm
dau = cay ra <=> x=y=z=1/3
Đúng 0
Bình luận (0)
Tìm GTNN của:
a,\(x^2-4x+y^2-2y+10\)
b,\(x^2+y^2-x+6y+15\)
c,\(x^2+2y^2-6x-8y+2xy+5\)
a)\(x^2-4x+y^2-2y+10=\left(x^2-4x+4\right)+\left(y^2-2y+1\right)+5\)
\(=\left(x-2\right)^2+\left(y-1\right)^2+5\ge5\)
Dấu "=" xảy ra khi x=2;y=1
b) tương tự câu a
Đúng 0
Bình luận (0)
c)\(x^2+2y^2-6x-8y+2xy+5=x^2+2y^2+2x\left(y-3\right)-8y+5\)
\(=x^2+2x\left(y-3\right)+\left(y^2-6x+9\right)+\left(y^2-2x+1\right)-5\)
\(=x^2+2x\left(y-3\right)+\left(y-3\right)^2+\left(y-1\right)^2-5\)
\(=\left(x+y-3\right)^2+\left(y-1\right)^2-5\ge-5\)
Dấu "=" xảy ra khi x=2;y=1
Đúng 0
Bình luận (0)
tìm gtnn
d. D(x) = 2x² + 3y² + 4xy-8x-2y + 18 e. E(x) = 2x² + 3y² + 4z²-2(x+y+z) + 2 f F(x)=2x² +8xy + 11y2-4x-2y+6 g. G(x)=2x²+2y+z²+2xy-2xz-2yz-2x-4y h. H(x)=x² + y²-xy-x+y+1 Bài 2: Tim GTLN của các biểu thức sau a. A=4x²-5y² +8xy+10y+12
b.B=-x²-y²+xy+2x+2y
tìm gtnn
d. D(x) = 2x² + 3y² + 4xy-8x-2y + 18 e. E(x) = 2x² + 3y² + 4z²-2(x+y+z) + 2 f F(x)=2x² +8xy + 11y2-4x-2y+6 g. G(x)=2x²+2y+z²+2xy-2xz-2yz-2x-4y h. H(x)=x² + y²-xy-x+y+1 Bài 2: Tim GTLN của các biểu thức sau a. A=4x²-5y² +8xy+10y+12
b.B=-x²-y²+xy+2x+2y
tìm gtnn
d. D(x) = 2x² + 3y² + 4xy-8x-2y + 18 e. E(x) = 2x² + 3y² + 4z²-2(x+y+z) + 2 f F(x)=2x² +8xy + 11y2-4x-2y+6 g. G(x)=2x²+2y+z²+2xy-2xz-2yz-2x-4y h. H(x)=x² + y²-xy-x+y+1 Bài 2: Tim GTLN của các biểu thức sau a. A=4x²-5y² +8xy+10y+12
b.B=-x²-y²+xy+2x+2y
Ta có:
D=2x2+3y2+4xy−8x−2y+18C=2x2+3y2+4xy−8x−2y+18
D=2(x2+2xy+y2)+y2−8x−2y+18C=2(x2+2xy+y2)+y2−8x−2y+18
D=2[(x+y)2−4(x+y)+4]+(y2+6y+9)+1C=2[(x+y)2−4(x+y)+4]+(y2+6y+9)+1
D=2(x+y−2)2+(y+3)2+1≥1C=2(x+y−2)2+(y+3)2+1≥1
Dấu "=" xảy ra ⇔x+y=2⇔x+y=2và y=−3y=−3
Hay x = 5 , y = -3
Đc chx bạn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời