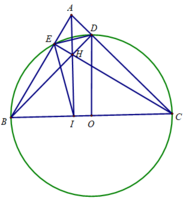
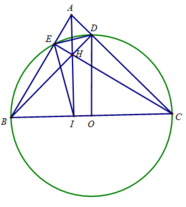
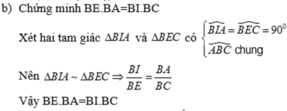Cho tam giác ABC nhọn . Đường tròn (O) đường kính BC cắt AB,AC lần lượt tại E và D.BD cắt CE tại H; AH cắt BC tại I.Vẽ cá tiếp tuyến AM và AN của (O) <M,N là các tiếp điểm >.CMR: M.H,N thẳng hàng.

Những câu hỏi liên quan
cho tam giác nhọn ABC có AB < AC. Đường tròn O đường kính BC cắt AB, AC lần lượt tại E và D. BD cắt CE tại H. ED cắt BC tại S. AH cắt O tại K. Chứng minh: SK là tiếp tuyến O
Cho tam giác nhọn ABC (AB < AC). Đường tròn tâm O đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE; AH cắt BC tại I.
b) Chứng minh BE.BA = BI.BC
Cho tam giác nhọn ABC (AB < AC). Đường tròn tâm O đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE; AH cắt BC tại I.
c) Chứng minh tứ giác OIED nội tiếp.
Cho tam giác nhọn ABC (AB < AC). Đường tròn tâm O đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE; AH cắt BC tại I.
d) Cho biết BC = 16cm. Tính BE.BA + CD.CA
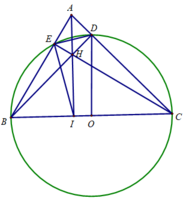
d) Tính BE.BA + CD.CA
Chứng minh tương tự câu b, CD.CA = CI.CB
Từ đó BE.BA + CD.CA = BI.BC + CI.CB
= (BI + CI).BC = BC.BC = B C 2 = 16 2 = 256
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn ( AB < AC ) .Đường tròn tâm O có đường kính BC cắt AB và AC lần lượt tại E và D . Gọi H là giáo điểm của CE và BD .
a ) AH cắt BC tại F : CMR AF vuông góc với BC
b) kẻ HK ⊥ OA tại K .C/m A,D,K,E cùng thuộc 1 đường tròn
Cho tam giác nhọn ABC (AB < AC). Đường tròn tâm O đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE; AH cắt BC tại I.
a) Chứng minh AI vuông góc với BC và EC là phân giác của góc IED.
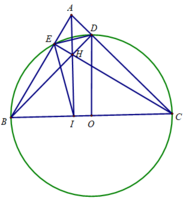
a) Chứng minh AI BC
Ta có ∠BEC = BDC = 90 0 (hai góc nội tiếp chắn nửa đườn tròn)

Đúng 0
Bình luận (0)
cho tam giác ABC nhọn (AB<AC). (O) đường kính BC cắt AC,AB lần lượt tại D,E. BD cắt CE tại H. AH cắt BC tại I, DE cắt BC tại F. Tiếp tuyến tại B của (O) cắt AF tại N, gọi J là tâm đường tròn ngoại tiếp tam giác FID. Chứng minh rằng: J,N,D thẳng hàng
Cho tam giác ABC nhọn đường tròn O đường kính BC cắt AB, AC lần lượt tại E và D,CE cắt BD tại H a) CM tứ giác ADHE nội tiếp b) AH cắt BC tại F. CM FA là tia p/giác góc DFE c) EF cắt đường tròn tại K. CM DK//AF d) cho bt góc BCD=45° ,BC=4 .Tín diện tích tam giác ABC
a: góc BEC=góc BDC=1/2*180=90 độ
=>CE vuông góc AB, BD vuông góc AC
góc AEH+góc ADH=180 độ
=>AEHD nội tiếp
b: góc EFH=góc ABD
góc DFH=góc ACE
mà góc ABD=góc ACE
nên góc EFH=góc DFH
=>FH là phân giác của góc EFD
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có ABAC. Vẽ đường tròn (O) đường kính BC cắt AB,AC lần lượt tại E,D. CE cắt BD tại H. AH cắt BC tại Ka. Chứng minh tứ giác BEHK nội tiếp và KA là phân giác góc EKDb. AI,AJ là các tiếp tuyến của (O) với tiếp điểm là I,J sao choD,J cùng nằm trên 1 nửa mặt phẳng bờ AK. Chứng minh góc IKE bằng góc DKJc. Chứng minh I,H,J thẳng hàngd. Kẻ đường thẳng qua K song song với ED cắt AB,CH lần lượt tại Q,S. Chứng minh K là trung điểm của QSAi giúp mình với :)))
Đọc tiếp
Cho tam giác ABC nhọn có AB<AC. Vẽ đường tròn (O) đường kính BC cắt
AB,AC lần lượt tại E,D. CE cắt BD tại H. AH cắt BC tại K
a. Chứng minh tứ giác BEHK nội tiếp và KA là phân giác góc EKD
b. AI,AJ là các tiếp tuyến của (O) với tiếp điểm là I,J sao choD,J cùng nằm trên 1 nửa
mặt phẳng bờ AK. Chứng minh góc IKE bằng góc DKJ
c. Chứng minh I,H,J thẳng hàng
d. Kẻ đường thẳng qua K song song với ED cắt AB,CH lần lượt tại Q,S. Chứng minh
K là trung điểm của QS
Ai giúp mình với :)))
a: góc BEH+góc BKH=180 độ
=>BEHK nội tiếp
=>góc EBH=góc EKH
góc BKA=góc BDA=90 độ
=>ABKD nội tiếp
=>góc EBH=góc AKD=góc EKH
=>KA là phân giác của góc EKD
b: góc AIO=góc AJO=góc AKO=90 độ
=>I,J,K,A,O cùng thuộc đường tròn đường kính OA
sđ cung AI=sđ cung AJ
=>góc AKI=góc AJI
=>góc AKE+góc IKE=góc AKD+góc DKJ
=>góc IKE=góc DKJ
c:
Đúng 0
Bình luận (0)