[Toán 7]Giá trị nhỏ nhất của x thõa mãn 5(x-2)(x+3)=1 ?

Những câu hỏi liên quan
Tập hợp các giá trị của x thõa mãn ( 2x +1 )left(3x-frac{9}{2}right) 0 là....Giá trị lớn nhất của biểu thức Q -2 . giá trị tuyệt đối của 3 - 0.25 . x bằng 7 là ...Tập hợp các số hữu tỉ thõa mãn đẳng thức x^2-25x^4 0 là ...Số giá trị của x thõa mãn x^2+7x+120là........Tập hợp các giá trị của x sao cho 5^{left(x+3right)left(2x-4right)}là...Giá trị nhỏ nhất của biểu thức B ( giá trị tuyệt đối của x +3 + 6 ) ^2 là...Giải chi tiết giùm mình, mình tick cho
Đọc tiếp
Tập hợp các giá trị của x thõa mãn ( 2x +1 )\(\left(3x-\frac{9}{2}\right)\)= 0 là....
Giá trị lớn nhất của biểu thức Q = -2 . giá trị tuyệt đối của 3 - 0.25 . x bằng 7 là ...
Tập hợp các số hữu tỉ thõa mãn đẳng thức \(x^2-25x^4\)= 0 là ...
Số giá trị của x thõa mãn \(x^2+7x+12=0\)là........
Tập hợp các giá trị của x sao cho \(5^{\left(x+3\right)\left(2x-4\right)}là\)...
Giá trị nhỏ nhất của biểu thức B = ( giá trị tuyệt đối của x +3 + 6 ) ^2 là...
Giải chi tiết giùm mình, mình tick cho
1,Tổng giá trị tuyệt đối của x thõa mãn -99 bé hơn hoặc bằng x bé hơn hoặc bằng 98
2,giá trị nguyên dương x thõa mãn |x-1|=-(x-1)
3, Giá trị lớn nhất của biểu thức |3-x|+4 là
4, Tổng bình phương của các sooso nguyên n thõa mãn -3<n<4
Có bao nhiêu số x∈Q thõa mãn |2x+3|+|5-3x|A. Không có B. Có 1 số C. Có 2 số D. Có 3 số2. Tìm giá trị nhỏ nhất của H|2x-3|-4A. H đạt giá trị nhỏ nhất là 2 B. H đạt giá trị nhỏ nhất là -3C. H đạt giá trị nhỏ nhất là 9 D. H đạt giá trị nhỏ nhất là -43. Tìm giá trị lớn nhất của H 8-|x+6|A. H đạt giá trị lớn nhất là 15 B. H đạt giá trị lớn nhất là 8B. _____________...
Đọc tiếp
Có bao nhiêu số x∈Q thõa mãn |2x+3|+|5-3x|
A. Không có B. Có 1 số C. Có 2 số D. Có 3 số
2. Tìm giá trị nhỏ nhất của H=|2x-3|-4
A. H đạt giá trị nhỏ nhất là 2 B. H đạt giá trị nhỏ nhất là -3
C. H đạt giá trị nhỏ nhất là 9 D. H đạt giá trị nhỏ nhất là -4
3. Tìm giá trị lớn nhất của H= 8-|x+6|
A. H đạt giá trị lớn nhất là 15 B. H đạt giá trị lớn nhất là 8
B. ____________________ 6 D. ____________________ 1
giá trị nguyên nhỏ nhất của x thõa mãn bất phương trình ( 2x-5)2 < ( 2x-1)(2x+ 1) - 5/4
hồi còn học lớp 8 mà hỏi câu j dễ quá vậy...h em đã học 11 r
Đúng 0
Bình luận (0)
làm sao để có thể nói với em rằng anh yêu nhiều ntn
Đúng 0
Bình luận (0)
Cho hai số thực x, y dương thõa mãn điều kiện x2 + y2 - xy = 4. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức : P = x2 + y2. (Trích đề thi HSG toán 9 tỉnh Bình Định năm học 2012-2013)
(Cho hai số thực dương x,y thõa mãn xy=1. Tìm giá trị nhỏ nhất của biểu thức: M=x2+y2+3/(x+y+1)
cho x, y là 2 số thực thõa mãn: x2 + 2y2 + 2xy + 7x +7y + 10 = 0
tìn giá trị nhỏ nhất và giá trị lớn nhất của biểu thức : A = x + y +1
Giá trị x nhỏ nhất thõa mãn x^4-13x^2+36=0
Cho các số thực x; y thõa mãn x≥0; y≥0 và x+y1. Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức
S
(
4
x
2
+
3
y
)
(
4
y
2
+
3
x
)
+
25
x
y
là: A.
M
25
2
;
m...
Đọc tiếp
Cho các số thực x; y thõa mãn x≥0; y≥0 và x+y=1. Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức S = ( 4 x 2 + 3 y ) ( 4 y 2 + 3 x ) + 25 x y là:
A. M = 25 2 ; m = 191 16 .
B. M = 12 ; m = 191 16 .
C. M = 25 2 ; m = 12 .
D. M = 25 2 ; m = 0 .
Do x+ y= 1 nên
S = 16 x 2 y 2 + 12 ( x + y ) ( x 2 - x y + y 2 ) + 34 x y = 16 x 2 y 2 + 12 ( x + y ) 2 - 3 x y + 34 x y , d o x + y = 1 = 16 x 2 y 2 - 2 x y + 12
Đặt t= xy . Do x≥ 0 ; y≥0 nên
0 ≤ x y ≤ ( x + y ) 2 4 = 1 4 ⇒ t ∈ 0 ; 1 4
Xét hàm số f(t) = 16t2- 2t + 12 trên [0 ; 1/4].
Ta có f’ (t) = 32t- 2 ; f’(t) =0 khi t= 1/ 16 .
Bảng biến thiên
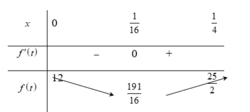
Từ bảng biến thiên ta có:
m i n 0 ; 1 4 f ( t ) = f ( 1 16 ) = 191 16 ; m a x 0 ; 1 4 f ( t ) = f ( 1 4 ) = 25 2
Vậy giá trị lớn nhất của S là 25/2 đạt được khi
x + y = 1 x y = 1 4 ⇔ x = 1 2 y = 1 2
giá trị nhỏ nhất của S là 191/ 16 đạt được khi
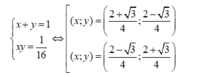
Chọn A.
Đúng 0
Bình luận (0)















