\(a.\)

Theo đề , ta có : \(y=f\left(x\right)=4x^2-5\)

\(\Rightarrow\)

\(f\left(3\right)=4.\left(3\right)^2-5=31\)

\(f\left(-\frac{1}{2}\right)=4.\left(-\frac{1}{2}\right)^2-5=-4\)

\(b.\)

Ta có : \(f\left(x\right)=-1\)

\(\Rightarrow4x^2-5=-1\)

\(\Rightarrow4x^2=-1+5=4\)

\(\Rightarrow x^2=4:4=1\)

\(\Rightarrow x=\sqrt{1}=1\)

\(c.\)

Ta có :

\(f\left(x\right)=4x^2-5\)

\(\Rightarrow f\left(x\right)=4.\left(x\right)^2-5\) \(\left(1\right)\)

\(f\left(-x\right)=4.\left(-x\right)^2-5=4.\left(x\right)^2-5\) \(\left(2\right)\)

Từ \(\left(1\right)\) và \(\left(2\right)\Rightarrow f\left(x\right)=f\left(-x\right)\)

a) Thay f(3) vào hàm số ta có :

y=f(3)=4.3²-5=31

Thay f(-1/2) vào hàm số ta có :

y=f(-1/2)=4.(-1/2)²-5=-4

b) Thay x=-1 vào hàm số ta có : 4.(-1)²-5=-1

=> f(-1) với x=-1

cam on nhe

tfyjtftftfkyh,hjgjfyhfj,fjghjgjfyfyjfjyhfjhyf,hfykfyffuyfh,jyfhjhjhfhjhhhhhcghgiufyf

a) +) \(f\left(-1\right)=\left(-4\right).\left(-1\right)+1=5\)

+) \(f\left(-\frac{1}{2}\right)=\left(-4\right).\left(-\frac{1}{2}\right)+1=3\)

b) +) y = 0

-4x + 1 = 0

-4x = 0 - 1

-4x = -1

x = 1/4

+) y = -3

-4x + 1 = -3

-4x = -3 - 1

-4x = -4

x = 1

Câu 5:

a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)

\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)

\(f\left(0\right)=7\cdot0-3=-3\)

b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:

\(2\left(2m+1\right)-3=3\)

=>2(2m+1)=6

=>2m+1=3

=>2m=2

=>m=1

c: Thay m=1 vào hàm số, ta được:

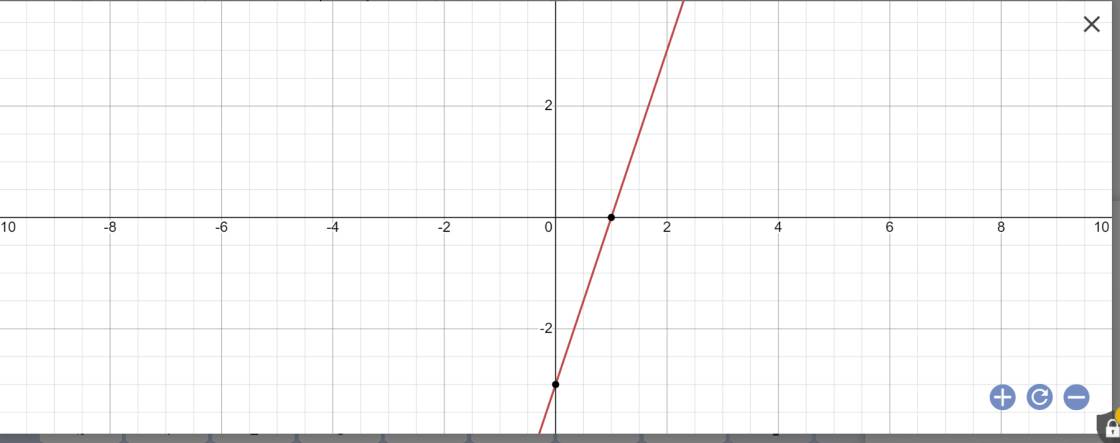
\(y=\left(2\cdot1+1\right)x-3=3x-3\)

*Vẽ đồ thị

d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)

=>\(2m\ne-1\)

=>\(m\ne-\dfrac{1}{2}\)

e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)

=>2m+1=5

=>2m=4

=>m=2

a: \(F\left(3\right)=3\left(3-2\right)=3\cdot1=3\)

\(\left[F\left(\dfrac{2}{3}\right)\right]^2=\left[\dfrac{2}{3}\cdot\left(\dfrac{2}{3}-2\right)\right]^2\)

\(=\left[\dfrac{2}{3}\cdot\dfrac{-4}{3}\right]^2=\left(-\dfrac{8}{9}\right)^2=\dfrac{64}{81}\)

\(G\left(-\dfrac{1}{2}\right)=-\left(-\dfrac{1}{2}\right)+6=6+\dfrac{1}{2}=\dfrac{13}{2}\)

b: F(x)=0

=>x(x-2)=0

=>\(\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

c: F(a)=G(a)

=>\(a\left(a-2\right)=-a+6\)

=>\(a^2-2a+a-6=0\)

=>\(a^2-a-6=0\)

=>(a-3)(a+2)=0

=>\(\left[{}\begin{matrix}a-3=0\\a+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=3\\a=-2\end{matrix}\right.\)

a) thay f(-2) vào hàm số ta có :

y=f(-2)=(-4).(-2)+3=11

thay f(-1) vào hàm số ta có :

y=f(-1)=(-4).(-1)+3=7

thay f(0) vào hàm số ta có :

y=f(0)=-4.0+3=-1

thay f(-1/2) vào hàm số ta có :

y=f(-1/2)=(-4).(-1/2)+3=5

thay f(1/2) vào hàm số ta có :

y=f(-1/2)=(-4).1/2+3=1

b)

f(x)=-1 <=> -4x+3=-1 => x=1

f(x)=-3 <=> -4x+3=-3 => x=3/2

f(x)=7 <=> -4x+3=7 => x=-1

Bạn ơi, f(0)= -4.0 + 3 =3 mà!

ukm đúng rồi bạn , mình quên