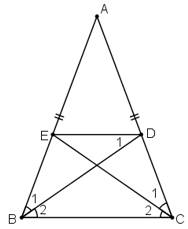
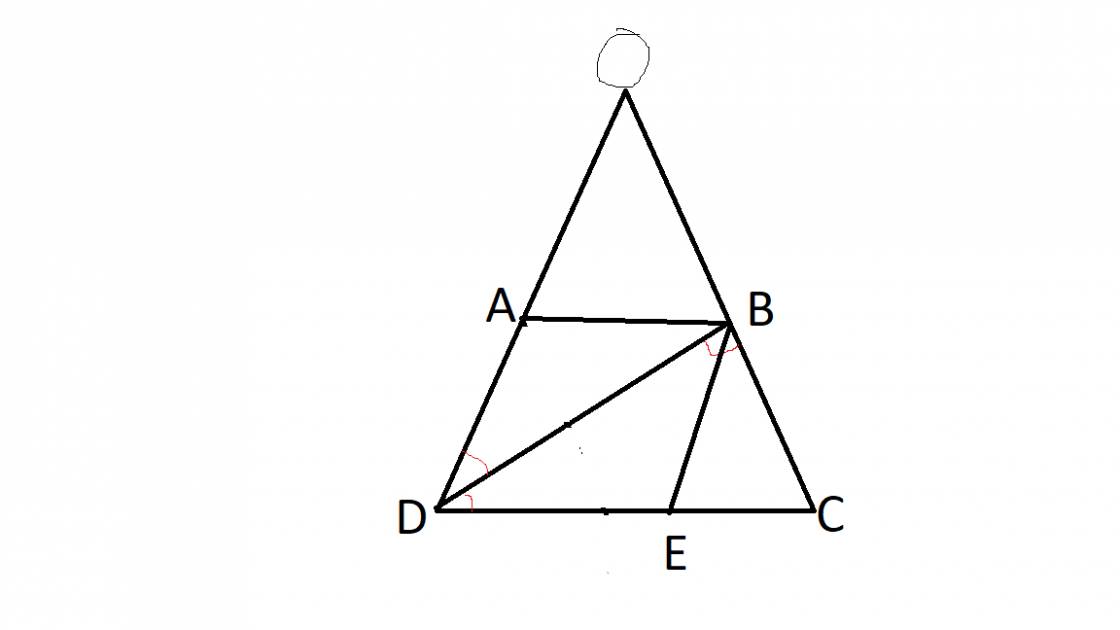
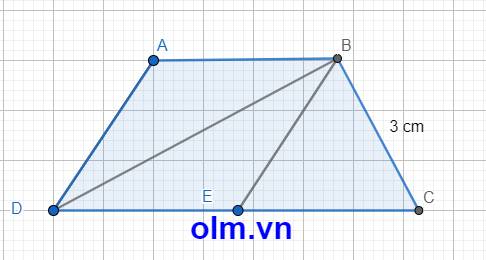
cho tam giác ABC vuông cân tại A cạnh bên=a ,vẽ hình chữ nhật AEMF có chu vi =2a (E thuộc AB; F thuộc AC)
a/ điểm M di động trên đường nào ?
b/ từ M vẽ MN vuông góc vs EF (N thuộc EF) C/M rằng MN luôn đi qua một điểm cố dịnh
mọi người giúp mình bài này nhá khó quá