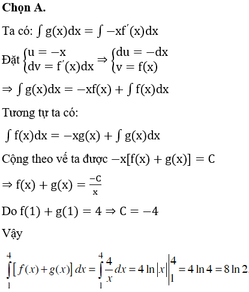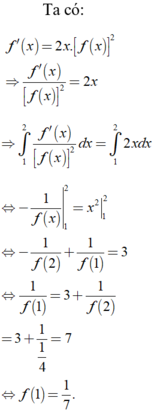cho hàm số y =f(x) thỏa mãn x.f(x)+f(\(\frac{1}{x}\)) =2x+1.Tính f(2)

Những câu hỏi liên quan
Cho hàm số y f(x) thỏa mãn
∫
0
π
2
sin
x
.
f
(
x
)
d
x
f
(
0
)
1
. Tính
I
∫
0
π
2
cos
x
.
f
(
x
)...
Đọc tiếp
Cho hàm số y = f(x) thỏa mãn ∫ 0 π 2 sin x . f ( x ) d x = f ( 0 ) = 1 . Tính I = ∫ 0 π 2 cos x . f ' ( x ) d x
A. I=1.
B. I=0.
C. I=2.
D. I=-1.
cho hàm số y=f(x) thỏa mãn f(x)-x.f(-x)=x+1 với mọi x thuộc Rtính f(1)
Cho hàm số y=f(x) thỏa mãn: 2.f(x)-x.f(x)=x+10(với mọi x thuộc R).Tính f(2).
Cho hàm số f(x) thỏa mãn x.f(x+2)=(x2-9). f(x).Tính f(5)
Với x=3 ta có
\(\Rightarrow3.f\left(3+2\right)=\left(3^2-9\right).f\left(3\right)\)
\(\Rightarrow3.f\left(5\right)=0\Rightarrow f\left(5\right)=0\)
Vậy f(5)=0
Cho hàm số f(x) và g(x) có đạo hàm trên đoạn [1;4] và thỏa mãn hệ thức:
f
(
1
)
+
g
(
1
)
4
g
(
x...
Đọc tiếp
Cho hàm số f(x) và g(x) có đạo hàm trên đoạn [1;4] và thỏa mãn hệ thức: f ( 1 ) + g ( 1 ) = 4 g ( x ) = - x . f ' ( x ) ; f ( x ) = - x . g ' ( x ) . Tính tích phân ∫ 1 4 [ f ( x ) + g ( x ) ] dx
A. 8ln2.
B. 3ln2
C. 6ln2
D. 4ln2
Cho hàm số f(x) xác định với mọi x thuộc R và thỏa mãn tính chất
(1-x^2).f(x)=x.f(x+1)
nhanh lên nha
Cho hàm số
y
f
(
x
)
thỏa mãn
f
(
2
)
1
4
và
f
(
x
)
2
x
.
[
f
(
x
)
]
2
với
∀
x
∈
R
tính...
Đọc tiếp
Cho hàm số y = f ( x ) thỏa mãn f ( 2 ) = 1 4 và f ' ( x ) = 2 x . [ f ( x ) ] 2 với ∀ x ∈ R tính f ( 1 )
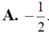
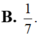
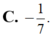
![]()
Cho đa thức f(x) thỏa mãn 2.f(x) - x.f(\(\frac{1}{x}\)) = x2. Tính f(2) và f(\(\frac{1}{3}\))
Ta có 2f(x)-x.f(1/x)=x^2
Với x=2 => 2f(2)-2.f(1/2)=4 (1)
Với x=1/2 => 2 . f(1/2)- 1/2 f(2) = (1/2)^2
=> 2 .f(1/2) -1/2f(2)=1/4(2)
lấy (2)+(1) ta được 3/2 f(2)=17/4 => f(2)=17/6
Tính f(1/3) làm tương tự thay x=3 và 1/3
T ic k nha
Đúng 0
Bình luận (0)
cho hàm số y=f(x) thỏa mãn: f(x) + 3.f(2x)= x+1. Tính f(10)