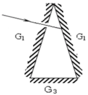
Vì sau khi phản xạ lần lượt trên các gương, tia phản xạ ló ra ngoài lỗ S trùng đúng với tia chiếu vào. Điều đó cho thấy trên từng mặt phản xạ có sự trùng nhau của tia tới và tia ló. Điều này chỉ xảy ra khi tia KR tới gương G₃ theo hướng vuông góc với mặt gương. Trên hình vẽ ta thấy 

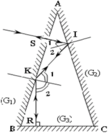
Tại I :  I ^ 1 = I ^ 2 = A ^  

Tại K:  K ^ 1 = K ^ 2

Mặt khác  K ^ 1 = I ^ 1 + I ^ 2 = 2 A ^

Do KR^BC  ⇒ K ^ 2 = B ^ = C ^

Þ B ^ = C ^ = 2 A ^

Trong DABC có   A ^ + B ^ + C ^ = 180 0

A ^ + 2 A ^ + 2 A ^ = 5 A ^ = 180 0 ⇒ A ^ = 180 0 5 = 36 0 ⇒ B ^ = C ^ = 2 A ^ = 72 0

chúc bạn học tốt1

Hok tốt

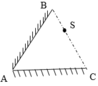
Vẽ hình:

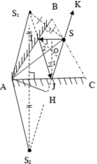
a) S₁ là ảnh của S qua gương AB => S₁ đối xứng với S  qua AB    

    S₂ là ảnh của S₁ qua gương AC => S₂ đối xứng với S ₁ qua AC  

Ta nối S₂ với S cắt AC tại J, nối J với S₁ cắt AB tại I

=> SI, IJ, JS là ba đoạn của tia sáng cần dựng.                        

b) Dựng hai phỏp tuyến tại I và J cắt nhau tai O

     Góc tạo bởi tia phản xạ JK và tia tới SI là  ∠  ISK

Theo tính chất góc ngoài tam giác ta có

  I S K ^ = I ^ + J ^ = 2 I ^ 2 + 2 J ^ 2 = 2 ( 180 0 − I O ^ J ) = 2. B A ^ C = 120 0

c) Tổng độ dài ba đoạn:

SI + IJ + JS = S₁I + IJ + JS = S₁J + JS = S₂J + JS = S₂S

(Đối xứng trục)

Vậy SI + IJ + JS = S₂S                                           

Ta có: 

∠  S₁AS =  2  ∠  S₁AB       (1)                             

           ∠  S₁AS₂ = 2  ∠  S₁AC        (2)                            

Lấy (2) – (1):

           ∠  S₁AS₂ -  ∠  S₁AS = 2( ∠  S₁AC -  ∠  S₁AB)

ð  ∠  SAS₂ = 2  ∠ BAC

ð  ∠ SAS₂ = 120⁰                                               

Xét tam giác cân SAS₂ tại A, có  ∠ A = 120⁰

ð   ∠  ASH = ∠  AS₂H = 30⁰ với đường cao AH, ta có:  SS₂ = 2SH        

Xét tam giác vuông SAH taị H có  ∠  ASH = 30⁰ ta có: AH = AS/2

Trong tam giác vuông SAH tại H. 

Theo định lí pitago ta tính được SH= S A . 3 2

 nên SS₂ = 2SH   =  2. S A . 3 2  = SA 3  

=> SS₂ nhỏ nhất ó SA nhỏ nhất ó AS là đường cao của tam giác đều ABC

ó S là trung điểm của BC.                                                                      

các bạn giúp mình với cần gấp quá

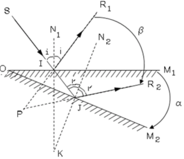
         * Xét gương quay quanh trục O từ vị trí M₁ đến vị trí M₂ (Góc M₁O M₁ = a) lúc đó pháp tuyến cũng quay 1 góc N₁KN₂ = a (Góc có cạnh tương ứng vuông góc).

         * Xét DIPJ có:

Góc IJR₂ = ∠ J I P + ∠ I P J  hay:

2i^’ = 2i + b Þ b = 2(i^’-i)     (1)

         * Xét DIJK có

      ∠ I J N 2 = ∠ J I K + ∠ I K J  hay

     i^’ = i + a Þ  a = 2(i^’-i)     (2)

Từ (1) và (2) ta suy ra b = 2a

     Tóm lại: Khi gương quay một góc a quanh một trục bất kì  thì tia phản xạ sẽ quay đi một góc 2a theo chiều quay của gương