Hai gương phẳng giống nhau AB và AC được đặt hợp với nhau một góc 600, mặt phản xạ hướng vào nhau (A,B,C tạo thành tam giác đều). Một nguồn sáng điểm S di chuyển trên cạnh BC. Ta chỉ xét trong mặt phẳng hình vẽ.
a) Hãy nêu cách vẽ đường đi của tia sáng phát ra từ S, phản xạ lần lượt trên AB, AC rồi về S.
b) Hãy tính góc tạo bởi tia tới từ S đến gương AB và tia phản xạ cuối cùng.
c) Với vị trí nào của S trên BC thì tổng đường đi của tia sáng trong câu a) là bé nhất?
Vẽ hình:
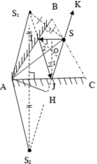
a) S1 là ảnh của S qua gương AB => S1 đối xứng với S qua AB
S2 là ảnh của S1 qua gương AC => S2 đối xứng với S 1 qua AC
Ta nối S2 với S cắt AC tại J, nối J với S1 cắt AB tại I
=> SI, IJ, JS là ba đoạn của tia sáng cần dựng.
b) Dựng hai phỏp tuyến tại I và J cắt nhau tai O
Góc tạo bởi tia phản xạ JK và tia tới SI là ∠ ISK
Theo tính chất góc ngoài tam giác ta có
I S K ^ = I ^ + J ^ = 2 I ^ 2 + 2 J ^ 2 = 2 ( 180 0 − I O ^ J ) = 2. B A ^ C = 120 0
c) Tổng độ dài ba đoạn:
SI + IJ + JS = S1I + IJ + JS = S1J + JS = S2J + JS = S2S
(Đối xứng trục)
Vậy SI + IJ + JS = S2S
Ta có:
∠ S1AS = 2 ∠ S1AB (1)
∠ S1AS2 = 2 ∠ S1AC (2)
Lấy (2) – (1):
∠ S1AS2 - ∠ S1AS = 2( ∠ S1AC - ∠ S1AB)
ð ∠ SAS2 = 2 ∠ BAC
ð ∠ SAS2 = 1200
Xét tam giác cân SAS2 tại A, có ∠ A = 1200
ð ∠ ASH = ∠ AS2H = 300 với đường cao AH, ta có: SS2 = 2SH
Xét tam giác vuông SAH taị H có ∠ ASH = 300 ta có: AH = AS/2
Trong tam giác vuông SAH tại H.
Theo định lí pitago ta tính được SH= S A . 3 2
nên SS2 = 2SH = 2. S A . 3 2 = SA 3
=> SS2 nhỏ nhất ó SA nhỏ nhất ó AS là đường cao của tam giác đều ABC
ó S là trung điểm của BC.











