Trên mặt phẳng cho tia Ax . Có thể vẽ được mấy tia Ay sao cho xA y = 50o

Những câu hỏi liên quan
Trên mặt phẳng cho tia Ax. Có thể vẽ được mấy tia Ay sao cho góc xAy = 50o.
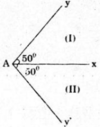
Có thể vẽ được hai tia như hình dưới để góc xAy = 50o.
Đúng 0
Bình luận (0)
Trên mặt phẳng ,cho tia Ax. Có thể vẽ được mấy tia Ay sao cho xAy= 50 độ
Trên mặt phẳng ,cho tia Ax .Có thể vẽ được mấy tia Ay sao cho góc xAy=50 độ
CÓ 2 CÁCH VẼ TIA Ay SAO CHO \(\widehat{xAy}=50^o\)
Cách 1:
Cách 2:
Đúng 0
Bình luận (0)
Có thể vẽ được 1 tia Ay sao cho góc xAy= 50 độ
Đúng 0
Bình luận (0)
Trên mặt phẳng, cho tia Ax. Có thể vẽ được mấy tia Ay sao cho \(\widehat{xAy}=50^0\) ?
Giải:
Có thể vẽ được hai tia như hình bên.
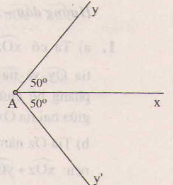
Đúng 0
Bình luận (1)
Trên mặt phẳng cho tia Ax. Có thể vẽ được mấy tia Ay sao cho góc xAy = 90 độ. Có nhận xét gì về quan hệ giữa các tia đó
Trên mặt phẳng Ax, có thể vẽ được 2 tia Ay sao cho \(\widehat{xAy}\)=90o.
Nhận xét: Hai tia này nằm trên 2 nửa mặt phẳng đối nhau bờ Ax, là 2 tia đối
Học tốt!!
#Bo
Cho tam giác ABC có ∠A=80o, ∠B=50o. Trên tia đối của tia AB lấy điểm O. Trên nửa mặt phẳng bờ AB ko chứa điểm C, vẽ tia Ox sao cho ∠BOx=50o. Gọi tia Ay là tia phân giác ∠CAO. Chứng minh: Ox//Bc, Ay//Bc
Cho tam giác ABC trên nửa mặt phẳng ko chứa B có bờ AC, vẽ tia Ax trên nửa mặt phẳng ko chứa C có bờ AB, vẽ tia Ay sao cho BAy=CAx, trên tia Ax lấy D sao cho AD=AC, trên tia Ay lấy E sao cho AE=AB. Chứng minh tam giác EAC=tam giác BAD; BD=CE.
Xét \(\Delta EAC\) và \(\Delta BAD\) có :
AD = AC ( gt )
\(\widehat{CAE}=\widehat{DAB}\)( hai góc đối đỉnh )
AE = AB ( gt )
nên \(\Delta EAC=\Delta BAD\left(c.g.c\right)\)
=> BD = CE ( hai cạnh tương ứng )
Đúng 0
Bình luận (0)
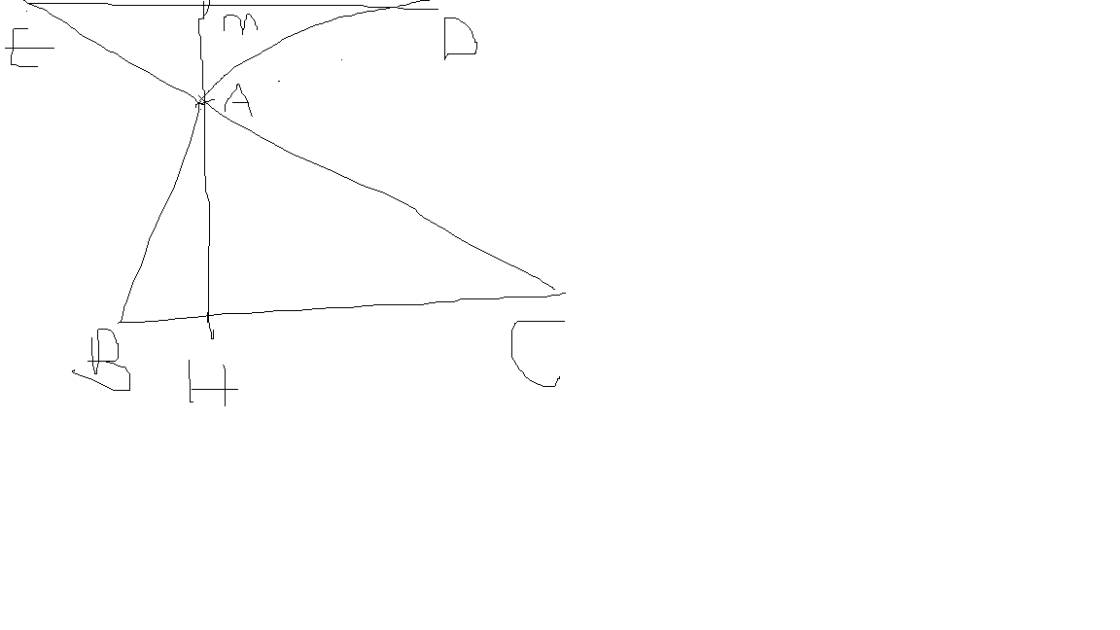
:Cho tam giác ABC nhọn. Trên nửa mặt phẳng bờ AC ko chứa B, vẽ tia Ax vuông góc với AC. Trên nửa mặt phẳng bờ AB ko chứa C, vẽ tia Ay vuông góc với AB.Trên tia Ax lấy điểm D sao cho AD=AC. Trên tia Ay lấy điểm E sao cho AE=AB.Kẻ AH cắt BC tại H. Tia đối của AH cắt ED tại M ME=MD
cho tam giác ABC có góc A<90 độ. Trên nửa mặt phẳng bờ AB chứa điểm C vẽ tia Ax vuông góc với AB, trên tia Ax lấy D sao cho AD=AB. Trên nửa mặt phẳng bờ AC có chứa B vẽ tia Ay vuông góc với AC, trên tia Ay lấy E sao cho AE=AC. Gọi M là trung điểm của BC. CM:AM=DE/2
Xem thêm câu trả lời