Cho Δ ABC có A(-1;4), B(2,3), C(0,1)
a) lập pt tham số đường thẳng chứa cạnh AB
b) lập pt tổng quát đường cao BH
c) lập pt tổng quát trung tuyến CM
d) tìm tâm đường tròn ngoại tiếp Δ ABC
các bạn hãy giải giúp mình nhé!!!
Bài 1: Cho Δ ABC vuông góc tại A có BC = 5cm, AC = 3cm, EF = 3cm, DE = DF = 2,5cm. Chọn phát biểu đúng?
A. Δ ABC ∼ Δ DEF
B. ABCˆ = EFDˆ
C. ACBˆ = ADFˆ
D. ACBˆ = DEFˆ
Bài 2: Cho hai tam giác Δ RSK và Δ PQM có: RS/PQ = RK/PM = SK/QM thì:
A. Δ RSK ∼ Δ PQM
B. Δ RSK ∼ Δ MPQ
C. Δ RSK ∼ Δ QPM
D. Δ RSK ∼ Δ QMP
Bài 3: Nếu Δ RSK ∼ Δ PQM có: RS/PQ = RK/PM = SK/QM thì
A. RSKˆ = PQMˆ
B. RSKˆ = PMQˆ
C. RSKˆ = MPQˆ
D. RSKˆ = QPMˆ
Bài 4: Chọn câu trả lời đúng?
A. Δ ABC, Δ DEF;AB/DE = AC/DF;Bˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
B. Δ ABC, Δ DEF;AB/DE = AC/DF;Cˆ = Fˆ ⇒ Δ ABC ∼ Δ DEF
C. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Dˆ ⇒ Δ ABC ∼ Δ DEF
D. Δ ABC, Δ DEF;AB/DE = AC/DF;Aˆ = Eˆ ⇒ Δ ABC ∼ Δ DEF
Bài 5: Cho hình bên, ABCD là hình thang ( AB//CD ) có AB = 12,5cm; CD = 28,5cm; DABˆ = DBCˆ. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
A. 17,5 B. 18
C. 18,5 D. 19
II. Bài tập tự luận
Bài 1: Tứ giác ABCD có AB = 2cm; BC = 6cm; CD = 8cm; DA = 3cm và BD = 4cm. Chứng minh rằng:
a) Δ BAD ∼ Δ DBC
b) ABCD là hình thang
Cho tam giác ABC có các đỉnh A(1;0), B(2;-3), C(-2;4) và đường thẳng Δ: x - 2y + 1 = 0. Đường thẳng Δ cắt cạnh nào của tam giác ABC?
A. AB và BC
B. AB và AC
C. AC và BC
D. Δ không cắt cạnh ΔABC
Đáp án: C
Thay lần lượt tọa độ của ba điểm A, B, C vào đường thẳng Δ ta được:
A: 1 - 2.0 + 1 = 2 > 0
B: 2 - 2.(-3) + 1 = 9 > 0
C: -2 - 2.4 + 1 = -9 < 0
Ta thấy: A và C nằm khác phía so với Δ nên Δ cắt cạnh AC
B và C nằm khác phía so với Δ nên Δ cắt cạnh BC
Cho Δ ABC vuông tại A, có đáy BC = 5cm và AB = 4cm. Diện tích Δ ABC là ?
A. 24 c m 2
B. 12 c m 2
C. 6 c m 2
D. 14 c m 2
Cho Δ ABC vuông tại A, có đáy BC = 5cm và AB = 4cm. Diện tích Δ ABC là ?
A. 24 c m 2
B. 12 c m 2
C. 6 c m 2
D. 14 c m 2
Cho Δ ABC,Δ A'B'C' có độ dài các cạnh như hình vẽ. Chứng minh Δ ABC ∼ Δ A'B'C'
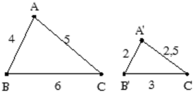
Xét Δ ABC,Δ A'B'C' có A'B'/AB = A'C'/AC = B'C'/BC = 2/4 = 2,5/5 = 3/6 = 1/2.
⇒ Δ ABC ∼ Δ A'B'C' ( c - c - c )
Cho Δ ABC,Δ A'B'C' có độ dài các cạnh như hình vẽ. Chứng minh Δ ABC ∼ Δ A'B'C'
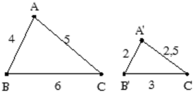
Xét Δ ABC,Δ A'B'C' có A'B'/AB = A'C'/AC = B'C'/BC = 2/4 = 2,5/5 = 3/6 = 1/2.
⇒ Δ ABC ∼ Δ A'B'C' ( c - c - c )
Cho Δ ABC có 3 đường cao AK,BM,CN cắt nhau tại H.
a) C/m: Δ ANH ~ Δ CKH, suy ra HA.HK = HN.HC
b) Δ HNK ~ Δ HAC và CN là phân giác của góc MNK
c) C/m: \(\dfrac{HK}{AK}+\dfrac{HM}{BM}+\dfrac{HN}{CN}=1\)
a: Xét ΔHNA vuông tại N và ΔHKC vuông tại K có
\(\hat{NHA}=\hat{KHC}\) (hai góc đối đỉnh)
Do đó: ΔHNA~ΔHKC
=>\(\frac{HN}{HK}=\frac{HA}{HC}\)
=>\(\frac{HN}{HA}=\frac{HK}{HC}\)
=>\(HN\cdot HC=HK\cdot HA\)
b: Xét ΔHNK và ΔHAC có
\(\frac{HN}{HA}=\frac{HK}{HC}\)
góc NHK=góc AHC
Do đó: ΔHNK~ΔHAC
=>\(\hat{HNK}=\hat{HAC}\)
=>\(\hat{CNK}=\hat{CAK}\)
mà \(\hat{CAK}=\hat{CBH}\left(=90^0-\hat{ACB}\right)\)
nên \(\hat{HNK}=\hat{CBH}\) (1)
Xét ΔHNB vuông tại N và ΔHMC vuông tại M có
\(\hat{NHB}=\hat{MHC}\) (hai góc đối đỉnh)
Do đó: ΔHNB~ΔHMC
=>\(\frac{HN}{HM}=\frac{HB}{HC}\)
=>\(\frac{HN}{HB}=\frac{HM}{HC}\)
Xét ΔHNM và ΔHBC có
\(\frac{HN}{HB}=\frac{HM}{HC}\)
\(\hat{NHM}=\hat{BHC}\) (hai góc đối đỉnh)
Do đó: ΔHNM~ΔHBC
=>\(\hat{HNM}=\hat{HBC}\) (2)
Từ (1),(2) suy ra \(\hat{CNM}=\hat{CNK}\)
=>NC là phân giác của góc MNK
c: Xét ΔHBC có HK là đường cao
nên \(S_{HBC}=\frac12\cdot HK\cdot BC\left(3\right)\)
Xét ΔABC có AK là đường cao
nên \(S_{ABC}=\frac12\cdot AK\cdot BC\left(4\right)\)
Từ (3),(4) suy ra \(\frac{S_{HBC}}{S_{ABC}}=\frac{\frac12\cdot HK\cdot BC}{\frac12\cdot AK\cdot BC}=\frac{HK}{AK}\)
Xét ΔHAC có HM là đường cao
nên \(S_{HAC}=\frac12\cdot HM\cdot AC\) (5)
Xét ΔBAC có BM là đường cao
nên \(S_{BAC}=\frac12\cdot BM\cdot AC\left(6\right)\)
Từ (5),(6) suy ra \(\frac{S_{HAC}}{S_{BAC}}=\frac{\frac12\cdot HM\cdot AC}{\frac12\cdot BM\cdot AC}=\frac{HM}{BM}\)
Xét ΔHAB có HN là đường cao
nên \(S_{HBA}=\frac12\cdot HN\cdot AB\) (7)
Xét ΔCAB có CN là đường cao
nên \(S_{CAB}=\frac12\cdot CN\cdot AB\) (8)
Từ (7),(8) suy ra \(\frac{S_{HBA}}{S_{CBA}}=\frac{\frac12\cdot HN\cdot AB}{\frac12\cdot CN\cdot AB}=\frac{HN}{CN}\)
\(\frac{HK}{AK}+\frac{HM}{BM}+\frac{HN}{CN}\)
\(=\frac{S_{HAB}+S_{HAC}+S_{HBC}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\)
Cho Δ ABC vuông tại A có cạnh AB = 3 cm;AC = 4 cm. Tính diện tích của tam giác Δ ABC ?
Cho Δ ABC và Δ MNP có A ^ = M ^ = 90 0 , AB/MN = BC/NP thì?
A. Δ ABC ∼ Δ PMN
B. Δ ABC ∼ Δ NMP
C. Δ ABC ∼ Δ MNP
D. Δ ABC ∼ Δ MPN
Ta có: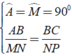
⇒ Δ ABC ∼ Δ MNP ( c - g - c )
Chọn đáp án C.
Cho Δ ABC vuông tại A có AB = 3 cm, BC = 5 cm, AD là đường phân giác của Δ ABC. Chọn phát biểu đúng?
A. BD = 20/7 cm; CD = 15/7 cm
B. BD = 15/7 cm; CD = 20/7 cm
C. BD = 1,5 cm; CD = 2,5 cm
D. BD = 2,5 cm; CD = 1,5 cm
Áp dụng định lý Py – ta – go ta có: A C = ( B C 2 - A B 2 ) = ( 52 - 32 ) = 4 ( c m )
Δ ABC, AD là đường phân giác của góc BACˆ ( D ∈ BC )
Ta có: DB/DC = AB/AC hay DB/AB = DC/AC
Khi đó ta có: DB/DC = AB/AC ⇒ DB/( DB + DC ) = AB /( AB + AC )
hay DB/5 = 3/( 3 + 4) ⇒ DB = 15/7 cm; DC = 20/7 ( cm )
Chọn đáp án B.