cho hai đường thẳng xy và xy' cắt nhau ở M và xMy' = 500. Số đo của góc x'My là;
A 1300 B 800 C 500 D 400
Những câu hỏi liên quan
Cho 2 đường thẳng xy và x'y' cắt nhau ở M và góc xMy' = 50 độ. Số đo của góc x'My là bao nhiêu ?
A.40 độ B. 50 độ C.80 độ D.130 dộ
Cho hai đường thẳng xy và kt cắt nhau tại A. Biết tổng số đo hai góc xAk và góc yAt là 60*. Tính số đo bốn góc A được tạo thành ?
Cho hai đường thẳng xy và st cắt nhau tại O, trong các góc tạo thành có góc 40o. Vẽ một đường tròn tâm O. Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.
Cho hai đường thẳng xy và st cắt nhau tại O, trong các góc tạo thành có góc 40 ° . Vẽ một đường tròn tâm O. Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.
Vẽ hai đường thẳng ab và xy cắt nhau tại M. Biết
a
M
x
^
56
°
. Tính số đo các góc xMb; bMy và aMy.
Đọc tiếp
Vẽ hai đường thẳng ab và xy cắt nhau tại M. Biết a M x ^ = 56 ° . Tính số đo các góc xMb; bMy và aMy.
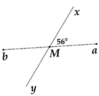
Vì tổng hai góc bù nhau là 180° nên ta tính được b M y ^ = 124 ° v à b M y ^ = 56 ° .
Đúng 0
Bình luận (0)
B1: Cho góc AOB = 50độ. Vẽ tia OC sao cho góc AOC = 75độ.
Tính số đo góc BOC.
B2: Cho 2 điểm A và B thuộc hai nửa mặt phẳng đối nhau bờ là đường thẳng xy (2 điểm A và B ko thuộc xy). Đoạn thẳng AB cắt xy tại M.
a) Cho biết góc AMy = 150độ. Hãy tính số đo góc AMx và góc BMy
b) Trên tia Mx lấy điểm O. Giả sử góc AOB = 60độ, góc AOy = 40độ. Tính góc BOx
Cho hai đường thẳng xy và x’y’ cắt nhau tại O và góc x’Oy= 45 độ . Hãy nêu tên các cặp góc đối đỉnh và tính số đo của các góc còn lại?
Xem chi tiết
các cặp góc đối đỉnh là \(\widehat{xOy}và\widehat{x'Oy'}\) ;\(\widehat{x'Oy}=\widehat{xOy'}\)
ta có \(\widehat{xOy}và\widehat{x'Oy'}\) là 2 góc đối đỉnh \(\Rightarrow\text{ }\text{ }\widehat{xOy}=\widehat{x'Oy'}=45độ\)
ta có \(\widehat{x'Oy}+\widehat{xOy}=180độ\)
\(\Rightarrow\widehat{x'Oy}+45độ=180độ\)
\(\Rightarrow\widehat{x'Oy}=180độ-45độ=135độ\)
ta có \(\widehat{x'Oy}=\widehat{xOy'}\) là 2 góc đối đỉnh
\(\Rightarrow\widehat{x'Oy}=\widehat{xOy'}=135độ\)
vậy \(\widehat{x'Oy}=135độ;\widehat{xOy'}=135độ;\widehat{x'Oy'}=45độ\)
Đúng 1
Bình luận (0)
Cho hai đường thẳng xy và x'y' phân biệt. Hãy nêu cách nhận biết xem hai đường thẳng xy và x'y' song song hay cắt nhau bằng dụng cụ thước đo góc
Cho hai đường thẳng xy và st cắt nhau tại O, trong các góc tạo thành có góc 40o. Vẽ một đường tròn tâm O. Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.
Ta có :
\(\widehat{xOs}\)= 400(theo giải thiết)
\(\widehat{tOy}\)=400( đối đỉnh với \(\widehat{xOs}\))
\(\widehat{xOt}\) + \(\widehat{tOy}\)= 1800
\(\Rightarrow\widehat{xOt}\) = \(\widehat{tOy}\) \(=180^0-40^0=140^0\)
\(\widehat{yOs}=140^0\)(đối đỉnh với \(\widehat{xOt}\))
\(\widehat{xOy}=\widehat{sOt}=180^0\)
Đúng 0
Bình luận (0)
