Tìm x \(\in\)\(ℕ\)để:
(2.n + 1) \(⋮\)( 3 - n)
CẦN GẤP!!!!
Tìm n \(\in\)\(ℕ\)để \(\frac{2n-5}{n-3}\)\(-\)\(\frac{2n-1}{n-3}\)nhỏ hơn 0
Mik dg cần gấp, ai nhanh mik tick nha
Tìm n \(\in\)\(ℕ\)để \(\frac{2n-5}{n-3}\)\(+\)\(\frac{2n-1}{2n-3}\)nhỏ hơn 0
Các bn làm nhanh hộ mik nha, mik dg cần gấp, ai nhanh mik tick
Tìm n thuộc \(ℕ^∗\)để 7n \(+\)13 là mẫu số chung của 2 phân số \(\frac{n}{n+1}\)và \(\frac{3}{3n+1}\)
AI NHANH THÌ MIK TICK 2 CÁI NHA, MIK DG CẦN GẤP
Để thỏa mãn đề bài thì 7n+13 phải chia hết cho n+1 và 3n+1
Trước hết ta xét:\(7n+13⋮n+1\Rightarrow\left(7n+7\right)+6⋮n+1\Rightarrow7\left(n+1\right)+6⋮n+1\Rightarrow6⋮n+1\)
Mà \(n\inℕ^∗\Rightarrow n+1\inℕ^∗\)
\(\Rightarrow n+1\in\left\{2;3;6\right\}\Rightarrow n\in\left\{1;2;5\right\}\)
Lần lượt thay các giá trị của n vào 7n+13 và 3n+1 xem 7n+13 có chia hết cho 3n+1 không
Sau khi thử thì còn các giá trị n là 1;5 thỏa mãn
Vậy n=1 hoặc n=5
Để 7n +13 là mẫu số chung của \(\frac{n}{n+1}và\frac{3}{3n+1}\) thì 7n+13 phải chia hết cho n+1 và 3n+1
*Xét 7n+13\(⋮\)n+1(1)
+)Ta có:n+1\(⋮\)n+1
=>7.(n+1)\(⋮\)n+1
=>7n+7\(⋮\)n+1(2)
+)Từ (1) và (2)
=>(7n+13)-(7n+7)\(⋮\)n+1
=>7n+13-7n-7\(⋮\)n+1
=>6\(⋮\)n+1
=>n+1\(\in\)Ư(6)={\(\pm\)1;\(\pm\)2;\(\pm\)3}
=>n\(\in\){-2\(\notin\)N*;0\(\notin\)N*;-3\(\notin\)N*;1\(\in\)N*;-4\(\notin\)N*;2\(\in\)N*}
=>n\(\in\){1;2}(*)
*Xét 7n+13\(⋮\)3n+1
=>3.(7n+13)\(⋮\)3n+1
=>21n+39\(⋮\)3n+1(3)
+)Ta có:3n+1\(⋮\)3n+1
=>7.(3n+1)\(⋮\)3n+1
=>21n+7\(⋮\)3n+1(4)
+)Từ (3) và (4)
=>(21n+39)-(21n+7)\(⋮\)3n+1
=>21n+39-21n-7\(⋮\)3n+1
=>32\(⋮\)3n+1
=>3n+1\(\in\)Ư(32)={\(\pm\)1;\(\pm\)2;\(\pm\)4;\(\pm\)8;\(\pm\)16;\(\pm\)32}
+)Ta có bảng:
| 3n+1 | -1 | 1 | -2 | 2 | -4 | 4 | -8 | 8 | -16 | 16 | -32 | 32 |
| n | \(\frac{-2}{3}\)\(\notin\)N* | 0\(\notin\)N* | -1\(\notin\)N* | \(\frac{1}{3}\)\(\notin\)N* | \(\frac{-5}{3}\)\(\notin\)N* | 1\(\in\)N* | -3\(\notin\)N* | \(\frac{7}{3}\)\(\notin\)N* | -5\(\notin\)N* | 5\(\in\)N* | \(\frac{-31}{3}\)\(\notin\)N* | \(\frac{31}{3}\)\(\notin\)N* |
=>n\(\in\){1;5}(**)
+)Từ (*) và (**)
=>n=1
Vậy n=1
Chúc bn học tốt
Tìm x \(\in\)\(ℕ\) để
a)n2+ 1 \(⋮\)n-1
b) 4n-5 \(⋮\) 2n-1
phần b tham khảo ở đây nhé :
Câu hỏi của Nguyễn Sĩ Hải Nguyên - Toán lớp 6 - Học toán với OnlineMath
( https://olm.vn/hoi-dap/detail/45713562308.html)
Câu b:
Giải:
Ta có: 4n-5 = 2(2n-1)-5 chia hết 2n-1
mà 2(2n-1) chia hết cho 2n-1
Suy ra 5 cũng sẽ chia hết cho 2n-1 => 2n-1 thuộc Ư(5)
=> Ta có bảng sau
| 2n-1 | 5 | 1 |
| 2n | 6 | 2 |
| n | 3 | 1 |
Vậy n e { 3;1 }
\(a,\) \(\text{Bài giải}\)
\(\frac{n^2+1}{n-1}=\frac{n\left(n-1\right)+n+1}{n-1}=\frac{n\left(n-1\right)}{n-1}+\frac{n-1+2}{n-1}=n+\frac{n-1}{n-1}+\frac{2}{n-1}=n+1+\frac{2}{n-1}\)
\(n^2+1\text{ }⋮\text{ }n-1\text{ khi }2\text{ }⋮\text{ }n-1\)
\(\Leftrightarrow\text{ }n-1\inƯ\left(2\right)=\left\{\pm1\text{ ; }\pm2\right\}\)
| \(n-1\) | \(-1\) | \(1\) | \(-2\) | \(2\) |
| \(n\) | \(0\) | \(2\) | \(-1\) | \(3\) |
\(\Rightarrow\text{ }n\in\left\{0\text{ ; }2\text{ ; }-1\text{ ; }3\right\}\)
Tìm n ∈ ℕ đ ể 3 n + 4 ⋮ n + 1
Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Tách. Bước 2. Áp dụng tính chất chia hết của một tổng. Bước 3. Tìm n+1. Bước 4. Tìm n. |
Ta có: 3 n + 4 = 3 n + 3 + 1 = 3 n + 1 + 1 Để 3 n + 4 ⋮ n + 1 thì 1 ⋮ n + 1 ⇒ n + 1 = 1 ⇒ n = 0 |
Tìm giá trị của x∈ℕ để C 12x 150 66 chia hết cho 6m.n giúp mình với mình đang cần gấp
Cho dãy số u n thỏa mãn u 1 = 1 u n = 3 u n - 1 + 1 ∀ n ∈ ℕ , n ≥ 2 . Tìm giá trị nhỏ nhất của n để log 9 u n > 100
A. 102
B. 101
C. 202
D. 201
Chọn đáp án D
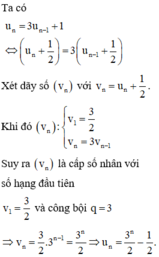
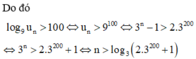
Vậy số tự nhiên n nhỏ nhất thỏa mãn điều kiện trên là n 0 = 201
Tìm x \(\in\) N để P \(\in\) N:
P=\(\left(\frac{3x+9\sqrt{x}-3}{x+\sqrt{x}-2}+\frac{1}{\sqrt{x}-1}+\frac{1}{\sqrt{x+2}}-2\right):\frac{1}{x-1}\)
(mình cần rất rất gấp, thank you)
Tìm n ∈ \(ℕ\), n ≥ 1 sao cho tổng 1! + 2! + 3! + ... + n! là 1 số chính phương
Xét các trường hợp:
\(n=1\Leftrightarrow1!=1=1^2\) là số chính phương
\(n=2\Leftrightarrow1!+2!=3\) không phải là số chính phương
\(n=3\Leftrightarrow1!+2!+3!=9=3^3\) là số chính phương
\(n\ge4\Leftrightarrow1!+2!+3!+4!=33\) còn \(5!,6!,7!,...,n!\) đều có tận cùng là \(0\Rightarrow1!+2!+3!+...+n!\) có tận cùng là chữ số 3 nên không phải là số chính phương
Vậy \(n\in\left\{1;3\right\}\).