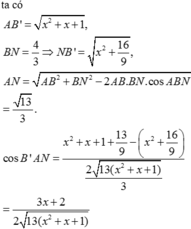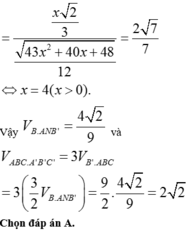Tam giác ABC ( góc A =90* ) ,1 tam giác vuông cân DAB . Cạnh hyền AB gọi là trung điểm BC. Tính BC

Những câu hỏi liên quan
cho tam giác ABC, góc A=90 độ có AB=8, BC=17. vẽ vào tam giác ABC 1 tam giác vuông cân, DAB có cạnh huyền AB. gọi E là trung điểm của BC. tính DE
bạn nào làm nhanh mk sẽ tik nha
Cho tam giác ABC vuông tại A có AB =8 ; BC = 17 . Vẽ trong tam giác ABC một tam giác vuông cân DAB có cạnh huyền là AB . Gọi E à trung điểm của BC . Tính DE
Theo đề bài ta có : \(\Delta DAB\)vuông cân tại D
\(\Rightarrow A_1=45^o\)( bù nhau )
Kéo dài BD cắt AC tại F .
Xét \(\Delta ABF\)có :
AD là đường phân giác đồng thời là đường cao
\(\Rightarrow\Delta ABF\)cân tại A
\(\Rightarrow AF=AB=8cm\)
Áp dụng định lí Py-ta-go ta có :
\(AC^2=BC^2-AB^2\)
\(\Rightarrow AC^2=17^2-8^2\)
\(\Rightarrow AC^2=225\)
\(\Rightarrow AC=\sqrt{225}=15\)
\(\Rightarrow CF=15-8=7cm\)
Xét tam giác BFC Có : \(EB=EC\left(gt\right)\)
\(DE//FC\)
=> DE là đường trung bình của tam giác BCF
\(\Rightarrow DE=\frac{1}{2}CF=3,5cm\)(T/c đường trung bình )
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A. AB=8cm, BC=17cm, vẽ vào trong tam giác ABC 1 tam giác vuông cân DAB có cạch huyền là AB. gọi e là trung điểm của BC. tính DE
Gọi M là trung điểm AB
Xét △△ vuông ABC (ˆA=90o)(A^=90o). Theo định lí Pytago ta có
AB2+AC2=BC2⟹AC2=BC2−AB2=172−82=225⟹AC=15AB2+AC2=BC2⟹AC2=BC2−AB2=172−82=225⟹AC=15
Xét △ABC△ABC có M là trung điểm AB, E là trung điểm BC \Rightarrow ME là đường trung bình của △ABC△ABC
\Rightarrow ME//AC,ME=12AC=7,5ME//AC,ME=12AC=7,5
Xét △ABD△ABD vuông tại D có DM là trung tuyến thuộc cạnh AB
⟹DM=12AB=4⟹DM=12AB=4
Do △ABD△ABD đều \Rightarrow trung tuyến DM còn là đường cao
⟹MD⊥AB⟹MD//AC⟹MD⊥AB⟹MD//AC
Do DM//AB,EM//AB⟹D,M,EDM//AB,EM//AB⟹D,M,E thẳng hàng
⟹DE=ME−DM=7,5−4=3,5⟹DE=ME−DM=7,5−4=3,5
Vậy DE=3,5 cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 8 cm ; BC = 10 cm . Vẽ trong tam giác ABC 1 tam giác vuông cân DAB có cạnh huyền AB . Gọi E là trung điểm BC . Tính DE ?
2K5 - IB - Kb nha - FA
#linhlunxinhcute :3
Haha bao nhiêu cx đc :D Mk đg cần ng tâm sự :3
Đúng 0
Bình luận (0)
Cho khối lăng trụ tam giác ABC.A′B′C′ có đáy là tam giác vuông tại A, AB 1,BC 2. Góc
∠
C
B
B
90
°
,
∠
A
B
B
120
°
. Gọi M là trung điểm cạnh AA′. Biết
d
A
B
,
C
M
7...
Đọc tiếp
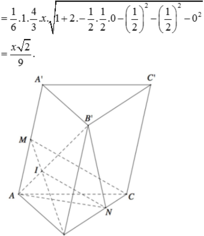
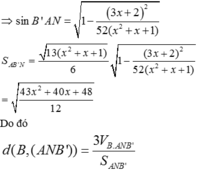
Cho khối lăng trụ tam giác ABC.A′B′C′ có đáy là tam giác vuông tại A, AB =1,BC = 2. Góc ∠ C B B ' = 90 ° , ∠ A B B ' = 120 ° . Gọi M là trung điểm cạnh AA′. Biết d A B ' , C M = 7 7 . Tính thể tích khối lăng trụ đã cho.
A. 2 2
B. 4 2 9
C. 4 2
D. 4 2 3
1)Cho tam giác ABC vuông cân tại A trên AB lấy D trên AC lấy E sao cho AD=AE qua D và A kẻ các đường thẳng vuông góc BE cắt BC tại I và K chứng minh IK=KC
2) cho tam giác ABC vuông tại A vẽ tam giác vuông cân DAB có cạnh huyền AB, E là trung điểm BC tính DE
1.Cho tam giác ABC ,A90.Biết AB+AC49cm,AB-AC7cm.Tính cạnh BC .2.Cho tam giác cân ABC, ABAC17cm.Kẻ BDvuôngAC.Tính cạnh đáy BC, biết BD15cm.3. Tính cạnh đáy BC của tam giác cân ABC, biết rằng đường vuông góc BH kẻ từ B xuống cạnh AC chia AC thành 2 phần:AH8cm,HC3cm.4. Một tam giác vuông có cạnh huyền là 102 cm, các cạnh góc vuông tỉ lệ với 8:5. Tính các cạnh của tam giác vuông đó.5. Cho tam giác ABC, biết BC bằng 52cm, AB 20cm ,AC48 cm.a, Chứng minh tam giác ABC vuông ở A;b, Kẻ AH vuông góc với...
Đọc tiếp
1.Cho tam giác ABC ,A=90.Biết AB+AC=49cm,AB-AC=7cm.Tính cạnh BC .
2.Cho tam giác cân ABC, AB=AC=17cm.Kẻ BDvuôngAC.Tính cạnh đáy BC, biết BD=15cm.
3. Tính cạnh đáy BC của tam giác cân ABC, biết rằng đường vuông góc BH kẻ từ B xuống cạnh AC chia AC thành 2 phần:AH=8cm,HC=3cm.
4. Một tam giác vuông có cạnh huyền là 102 cm, các cạnh góc vuông tỉ lệ với 8:5. Tính các cạnh của tam giác vuông đó.
5. Cho tam giác ABC, biết BC bằng 52cm, AB = 20cm ,AC=48 cm.
a, Chứng minh tam giác ABC vuông ở A;
b, Kẻ AH vuông góc với BC. Tính AH .
6. Cho tam giác vuông cân ABC, A=90.Qua A kẻ đường thẳng d tùy ý. Từ B và C kẻ BH vuông d. Chứng minh rằng tổng BH^2+CK^2 ko phụ thuộc vào vị trí của đường thẳng d.
7. Cho tam giác vuông ABC ,A= 90 độ. Trên nửa mặt phẳng bờ AC không chứa điểm B, kẻ tia CX sao cho CA là tia phân giác của gócBCx.Từ A kẻ AE vuông Có, từ B kẻ BD vuông AE. Gọi AH là đường cao của tam giác ABC. Chứng minh rằng :
a, A là trung điểm của DE
b, DHE=90 độ
8. Cho tam giác ABC có A bằng 90 độ,AB=8 cm,BC =17cm.Trên nửa mặt phẳng bờ AC ko chứa điểm B, vẽ tia CD vuông với AC và CD=36cm.Tính tổng độ dài các đoạn thẳngAB+BC+CD+DA.
Bài 1:
Độ dài cạnh AB: ( 49 + 7 ) : 2 = 28 (cm)
Độ dài cạnh AC: 28 - 7 = 21 (cm)
Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A có:
\(BC^2=AC^2+AB^2\)
Hay \(BC^2=21^2+28^2\)
\(\Rightarrow BC^2=441+784\)
\(\Rightarrow BC^2=1225\)
\(\Rightarrow BC=35\left(cm\right)\)
Đúng 0
Bình luận (0)
Bài 2:
Áp dụng định lý Py-ta-go vào tam giác ABD vuông tại D có:
\(AB^2=AD^2+BD^2\)
\(\Rightarrow AD^2=AB^2-BD^2\)
Hay \(AD^2=17^2-15^2\)
\(\Rightarrow AD^2=289-225\)
\(\Rightarrow AD^2=64\)
\(\Rightarrow AD=8\left(cm\right)\)
Trong tam giác ABC có:
\(AD+DC=AC\)
\(\Rightarrow DC=AC-AD=17-8=9\left(cm\right)\)
Áp dụng định lý Py-ta-go vào tam giác BCD vuông tại D có:
\(BC^2=BD^2+DC^2\)
Hay \(BC^2=15^2+9^2\)
\(\Rightarrow BC^2=225+81\)
\(\Rightarrow BC^2=306\)
\(\Rightarrow BC=\sqrt{306}\approx17,5\left(cm\right)\)
Đúng 0
Bình luận (0)
Bài 3:
Vì tam giác ABC cân tại A (gt) nên AB = AC
Mà AC = AH + HC
Hay AC= 8 + 3 = 11 (cm)
Nên AB = 11 (cm)
..........
( Phần này áp dụng định lý Py-ta-go vào tam giác và làm giống như bài 2 vậy nên mình không giải lại nữa nha bạn ) ( ^ o ^ )
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tai A , đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D , gọi M là trung điểm của cạnh BC . Chứng minh rằng :
a, Tam giác DAB và taM GIÁC dac
B, TAM GIÁC DBC cân
c, A , M ,D thẳng hàng
Cho tam giác vuông ABC có AB=8cm;BC=17cm.Vẽ vào bên trong tam giác ABC 1 tam giác vuông cân DAB có cạnh huyền AB.Gọi E là trung điểm BC.Tính DE
Gọi giao điểm của ED và AB là F.
Ta có: \(\Delta\)ABC vuông tại A , trung tuyến AE => AE=BE=CE
Xét \(\Delta\) AED và \(\Delta\)BED có:
AE=BE
DE chung => \(\Delta\)AED=\(\Delta\)BED (c.c.c)
AD=BD
=> ^AED=^BED (2 góc tương ứng) => ED là phân giác của ^AEB.
Mà \(\Delta\)AEB cân tại E (AE=BE) => ED là trung tuyến của \(\Delta\)AEB
Hay DF là trung tuyến của \(\Delta\)DAB. Do \(\Delta\)DAB vuông cân tại D => DF=1/2AB=8/2=4
Lại có: AC2=BC2-AB2=172-82=225 => AC=15 (cm)
E là trung điểm BC, F là trung điểm AB => EF là đường trung bình \(\Delta\)ABC
=> EF=AC/2=15/2=7,5 (cm)
=> DE=EF-DF=7,5-4=3,5 (cm)
Vậy DE=3,5cm.
Đúng 1
Bình luận (0)