cho tam giác ABC vuông tại A, có AB = 5cm, Ac = 12cm. Tính khoảng cách từ trọng tâm G đến đỉnh A

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, có AB=5cm , AC=12cm,. Tính khoảng cách từ trọng tâm G đến đỉnh A
Cho tam giác ABC vuông tại A. Trên tia đối của tia MA lấy điểm E sao cho M là trung điểm của AE.
a) Chứng minh EC vuông góc với AC
b) Chứng minh AM=1/2 BC
c) Cho biết AB=5cm, AC=12cm. Tính khoảng cách từ đỉnh A tới trọng tâm G của tam giác ABC
đề bài thiếu
Thiếu chỗ nào vậy bạn?
Bạn gì ơi, đề bài bị thiếu. Mọi người thêm vào M là trung điểm của BC nhé
cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Tính khoảng cách từ trọng tâm G của tam giác ABC tới các đỉnh A, B, C
cho tam giác ABC vuông tại A sao cho AB=16 cm ,AC = 30cm . tính tổng các khoảng cách từ trọng tâm G cuả tam giác đến các đỉnh của tam giác
Cho tam giác ABC vuông tại A, AB = 6 cm, AC = 8 cm. Tính khoảng cách từ trọng tâm G của tam giác ABC tới các đỉnh ABC
Gọi AM,BN,CE lần lượt là các đường trung tuyến của ΔABC
=>AM,BN,CE đồng quy tại G
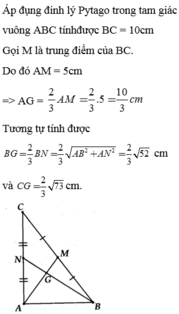
BC=căn 6^2+8^2=10cm
=>AM=5cm
=>AG=10/3cm
AN=8/2=4cm
=>BN=căn 6^2+4^2=2*căn 13(cm)
=>BG=2/3*2căn 13=4/3*căn 13(cm)
AE=6/2=3cm
CE=căn 3^2+8^2=căn 73(cm)
=>CG=2/3*căn 73(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , có AB = 16cm , AC = 30cm . Tính tổng các khoảng cách từ trọng tâm G của tgiác đến các đỉnh
Giúp mình nha =))
\(BC=\sqrt{AB^2+AC^2}\)
\(BC=\sqrt{16^2+30^2}\)
\(BC=34\left(cm\right)\)
Ta có: Tam giác ABC vuông tại A
\(MC=\sqrt{AC^2+AM^2}\)
\(MC=\sqrt{30^2+8^2}\)
\(MC=2\sqrt{241}\left(cm\right)\)
\(AM=\frac{1}{2}.BC=\frac{1}{2}.34=17\left(cm\right)\)
\(BD=\sqrt{AB^2+AD^2}\)
\(BD=\sqrt{16^2+15^2}=\sqrt{481}\left(cm\right)\)
Khoảng cách từ trọng tâm G của tam giác là: 2/3
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, AB = 6 cm, AC = 8 cm. Tính khoảng cách từ trọng tâm G của tam giác ABC tới các đỉnh, của tam giác.
cho tam giác ABC vuông ở A, AB=16cm, AC=30cm. Tính tổng các khoảng cách từ trọng tâm G của tam giác đến các đỉnh của tam giác.
Hình tự vẽ sắp phải đi học
\(BC=\sqrt{AB^2+AC^2}=\sqrt{16^2+30^2}=34\left(cm\right)\)
Ta có \(\Delta ABC\perp A\)( gt )
\(MC=\sqrt{AC^2+AM^2}=\sqrt{30^2+8^2}=2\sqrt{241}\left(cm\right)\)
\(AM=\frac{1}{2}.BC=\frac{1}{2}.34=17\left(cm\right)\)
\(BD=\sqrt{AB^2+AD^2}=\sqrt{16^2+15^2}=\sqrt{481}\)
Khoảng cách từ G đến các đỉnh bằng 2/3 khoảng cách đường trung tuyến
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4cm. Tính khoảng cách từ điểm A đến trọng tâm G của tam giác ABC
BC = \(\sqrt{3^2+4^2}\) = 5
Tam giác ABC vuông tại A => Trung tuyến AM = BC/2 = 5/2 cm
AG = 2AM/3 = 2/3 x 5/2 = 5/3 cm
Đúng 0
Bình luận (0)