gọi M là một của đoạn thẳng EF . Biết EM=4cm ,EF=8cm. So sánh hai đoạn thẳng EM và EF

Những câu hỏi liên quan
Gọi M là một điểm của đoạn thẳng EF. Biết EM = 4cm, EF = 8cm. So sánh hai đoạn thẳng EM và MF.
Vẽ hình: vì độ dài EM khác 0 và nhỏ hơn 8 cm nên M không trùng với hai đầu mút của đoạn thẳng EF (hay M nằm giữa E, F).
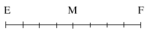
- Vì M nằm giữa E, F nên: EM + MF = EF
Suy ra: MF = EF - EM = 8 - 4 = 4 cm
Vì 4 = 4 nên EM = MF hay hai đoạn thẳng EM và MF có độ dài bằng nhau.
Đúng 1
Bình luận (0)
Gọi M là một điểm của đoạn thẳng EF. Biết EM = 4cm, EF = 8cm. So sánh hai đoạn thẳng EM và MF ?
Bài 47 Gọi M là một điểm của đoạn EF. Biết EM=4cm, EF=8cm. So sánh hai đoạn EM và EF.
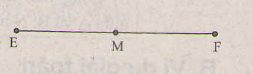
M là một điểm của đường đoạn thẳng EF, M không trùng với hai đầu đoạn thẳng vậy M nằm giữa E và F.
Ta có: EM+ MF= EF. Suy ra: EM=FM(= 4cm)
Đúng 0
Bình luận (0)
Gọi MM là một điểm của đoạn EFEF. Biết EM=4cm,EF=8cmEM=4cm,EF=8cm. So sánh hai đoạn EMEM và MFMF.
giúp mk nha
Gọi M là một điểm của đoạn thẳng EF.Biet EM=4cm,EF=8cm.So sánh hai đoạn thẳng EM va MF
Bài 1. Gọi M là một điểm của đoạn EF. Biết EM 4cm, EF 8cm. So sánh hai đoạn EM và EF.Bài 2. Em Hà có một sợi dây 1.25m. Em dùng sợi dây đó đo chiều rộng của lớp học. Sau bốn lần căng dây đo liên tiếp thì khoảng cách giữa hai đầu dây và mép tường còn lại bằng 1/5 độ dài sợi dây. Hỏi chiều rộng lớp học?Bài 3. Gọi M và N là hai điểm nằm giữa hai mút của đoạn thẳng AB, Biết rẳng AN BM. So sánh AM và BN. Xét cả hai trường hợp (h.25).Bài 4 . Cho ba điểm V,A,T thẳng hàng. Điểm nào nằm giữa hai điểm c...
Đọc tiếp
Bài 1. Gọi M là một điểm của đoạn EF. Biết EM= 4cm, EF = 8cm. So sánh hai đoạn EM và EF.
Bài 2. Em Hà có một sợi dây 1.25m. Em dùng sợi dây đó đo chiều rộng của lớp học. Sau bốn lần căng dây đo liên tiếp thì khoảng cách giữa hai đầu dây và mép tường còn lại bằng 1/5 độ dài sợi dây. Hỏi chiều rộng lớp học?
Bài 3.
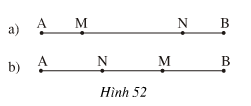
Gọi M và N là hai điểm nằm giữa hai mút của đoạn thẳng AB, Biết rẳng AN = BM. So sánh AM và BN. Xét cả hai trường hợp (h.25).
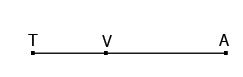
Bài 4 . Cho ba điểm V,A,T thẳng hàng. Điểm nào nằm giữa hai điểm còn lại nếu: TV + VA=TA
Câu 2:
Khoảng cách giữa đầu dây và mép tường còn lại là:
1,25 x \(\frac{1}{5}\) = 0,25 (m)
Khoảng cách 4 lần căng dây liên tiếp là:
1,25 x 4 = 5 (m)
Chiều rộng của lớp học là:
5 + 0,25 = 5,25 (m)
Đáp số:..................
Xét cả hai trường hợp sau:
a) Xét trường hợp điểm M nằm giữa hai điểm A và N; Điểm N nằm giữa hai điểm B và M.
( hình lấy mạng )
- Vì M nằm giữa A và M nên AN= AM+MN (1)
- Vi N nằm giữa B và M nên BM= BN + MN (2)
Mà AN= BM (đề bài) nên từ (1) và (2) suy ra AM + MN = BN + MN
Do đó: AM = BN.
b) Xét trường hợp điểm N nằm giữa A và M; điẻm M nằm giữa B và N.
( hình lấy mạng )
- Vì N nằm giữa A và M nên AN + NM= AM (3)
- Vì M nằm giữa B và N nên BM + MN= BN(4)
Mà AN=BM(Đề bài) nên từ (3) và(4) AM=BN
Trên một cạnh của một góc có đỉnh là A, đặt đoạn thẳng AE = 3cm và AC = 8cm, trên cạnh thứ hai của góc đó, đặt các đoạn thẳng AD = 4cm và AF = 6cm.
a) Hai tam giác ACD và AEF có đồng dạng không? Vì sao?
b) Gọi I là giao điểm của CD và EF. Tính tỉ số của hai tam giác IDF và IEC.
Mọi người giúp e với ạ!
Bài 4 :Trên một cạnh của một góc có đỉnh là A, đặt đoạn thẳng AE = 3cm, AC = 8cm, trên cạnh thứ hai của góc đó đặt các đoạn thẳng AD = 4cm, AF = 6cm
a) Hai tam giác ABC và AEF có đồng dạng không? vì sao?
b) Gọi I là giao điểm của CD và EF. Tính tỉ số của 2 tam giác IDF và IEC
a) Sửa đề:ΔADC và ΔAEF có đồng dạng không? Vì sao
Xét ΔADC và ΔAEF có
\(\dfrac{AD}{AE}=\dfrac{AC}{AF}\left(=\dfrac{4}{3}\right)\)
\(\widehat{DAC}\) chung
Do đó: ΔADC\(\sim\)ΔAEF(c-g-c)
b) Ta có: ΔADC\(\sim\)ΔAEF(cmt)
nên \(\widehat{ACD}=\widehat{AFE}\)(hai góc tương ứng)
hay \(\widehat{ICE}=\widehat{IFD}\)
Xét ΔICE và ΔIFD có
\(\widehat{EIC}=\widehat{DIF}\)(hai góc đối đỉnh)
\(\widehat{ICE}=\widehat{IFD}\)(cmt)
Do đó: ΔICE\(\sim\)ΔIFD(g-g)
Suy ra: \(\dfrac{S_{ICE}}{S_{IFD}}=\left(\dfrac{CE}{FD}\right)^2\)(Định lí)
\(\Leftrightarrow\dfrac{S_{ICE}}{S_{IFD}}=\left(\dfrac{5}{2}\right)^2=\dfrac{25}{4}\)
hay \(\dfrac{S_{IFD}}{S_{ICE}}=\dfrac{4}{25}\)
Đúng 4
Bình luận (0)
1.Trên tia Dx lấy 2 điểm E và F sao cho DE 2 cm; DF 6cma) Trong 3 điểm D; E;F điểm nào nằm giữa hai điểm còn lại. Vì sao?b) Tính độ dài đoạn thẳng EFc) Gọi I là trung điiềm của đoạn thẳng EF. Tinhs độ dài đoạn thẳng IF2.Cho đường thẳng xy và điểm A thuộc đường thẳng xy. Trên tia Ay vẽ 2 đoạn thẳng AB 5cm; AC 8cma)Tính độ dài đoạn thẳng BCb) trên tia đối của tia By vẽ đoạn thẳng BM 2cm. So sánh 2 đoạn thẳng AB và MC
Đọc tiếp
1.Trên tia Dx lấy 2 điểm E và F sao cho DE= 2 cm; DF= 6cm
a) Trong 3 điểm D; E;F điểm nào nằm giữa hai điểm còn lại. Vì sao?
b) Tính độ dài đoạn thẳng EF
c) Gọi I là trung điiềm của đoạn thẳng EF. Tinhs độ dài đoạn thẳng IF
2.Cho đường thẳng xy và điểm A thuộc đường thẳng xy. Trên tia Ay vẽ 2 đoạn thẳng AB= 5cm; AC= 8cm
a)Tính độ dài đoạn thẳng BC
b) trên tia đối của tia By vẽ đoạn thẳng BM= 2cm. So sánh 2 đoạn thẳng AB và MC
Gọi M là một điểm thuộc đoạn EF. Biết EM = 3cm, EF = 7cm . Độ dài của đoạn MF là:
A. 10cm
B. 4cm
C. 3cm
D. 7cm
Đáp án là B
Vì M là một điểm thuộc đoạn EF nên M nằm giữa E và F
⇒ EM + MF = EF
⇒ MF = EF - EM = 7 - 3 = 4 cm
Đúng 0
Bình luận (0)














