Cho 2 đường thẳng a và b. Cùng vuông góc với 1 đường thẳng c, tại A, B. Một đường thẳng d cắt a tại M và b tại N.
a, aMN = 142 độ. Tính MNb
b, 2 đường phân giác NMA, MNB cắt nhau tại P( P thuộc c). tính MPN
Cho 2 đường thẳng a và b. Cùng vuông góc với 1 đường thẳng c, tại A, B. Một đường thẳng d cắt a tại M và b tại N.
a, aMN = 142 độ. Tính MNb
b, 2 đường phân giác NMA, MNB cắt nhau tại P( P thuộc c). tính MPN
Cho 2 đường thẳng a và b. Cùng vuông góc với 1 đường thẳng c, tại A, B. Một đường thẳng d cắt a tại M và b tại N.
a, aMN = 142 độ. Tính MNb
b, 2 đường phân giác NMA, MNB cắt nhau tại P( P thuộc c). tính MPN
cho 2 đường thẳng a và b. Cùng vuông góc với đường thẳng c, tại A,B. Một đường thẳng d cắt a tại M và b tại N.
a, aMn = 142 độ. tính MNb
b, 2 đường phân giác NMA, MNB cắt nhau tại P( P thuộc C). Tính MPN
Cho hai đường thẳng a và b cùng vuông góc với đường thẳng d cắt a tại M và cắt b tại N
a, Góc aMN =142 độ , Tính MNb
b, Hai đường phân giác của Góc NMa, MNb cắt nhau tại P sao cho P thuộc C .Tính MPN
Cho hai đường thẳng a và b cùng vuông góc với đường thẳng d cắt a tại M và cắt b tại N
a, Góc aMN =142 độ , Tính MNb
b, Hai đường phân giác của Góc NMa, MNb cắt nhau tại P sao cho P thuộc C .Tính MPN
Cho tam giác ABCD vuông tại A, phân giác BF. Từ điểm I nằm giữa B và F vẽ đường thẳng song song với AC cắt AB, BC lần lượt tại M và N. Vẽ đường trong ngoại tiếp tam giác BIN cắt AI tại D. Hai đường thẳng DN và BF cắt nhau tại E. Chứng minh:
a, Bốn điểm A, B, D, E cùng thuộc một đường tròn
b, Năm điểm A, B, C, D, E cùng thuộc một đường tròn. Từ đó suy ra BE vuông góc với CE
a, Chứng minh: A B E ^ = A D E ^
b, Chứng minh được:
A
C
B
^
=
B
N
M
^
=> C, D, E nhìn AB dưới góc bằng nhau nên A, B, C, D, E cùng thuộc một đường tròn
=> BC là đường kính => B E C ^ = 90 0
Cho tam giác ABC vuông tại A. Biết AC = 12cm, BC = 15cm
a) Tính độ dài cạnh AB
b)Tia phân giác của góc B cắt AC tại M. Vẽ MN vuông góc với BC ( N thuộc BC ). Chứng minh AM=MN
c) Một đường thẳng qua C và vuông góc với đường thẳng BM tại E, cắt đường thẳng AB tại D. Chứng minh AD = NC
a: \(AB=\sqrt{15^2-12^2}=9\left(cm\right)\)
b: Xét ΔBAM vuông tại A và ΔBNM vuông tại N có
BM chung
góc ABM=góc NBM
=>ΔBAM=ΔBNM
=>MA=MN
c: Xét ΔBDC có
BE là đừog cao, là phân giác
nên ΔBDC cân tại B
=>BD=BC
BA+AD=BD
BN+NC=BC
mà BD=BC; BA=BN
nên AD=NC
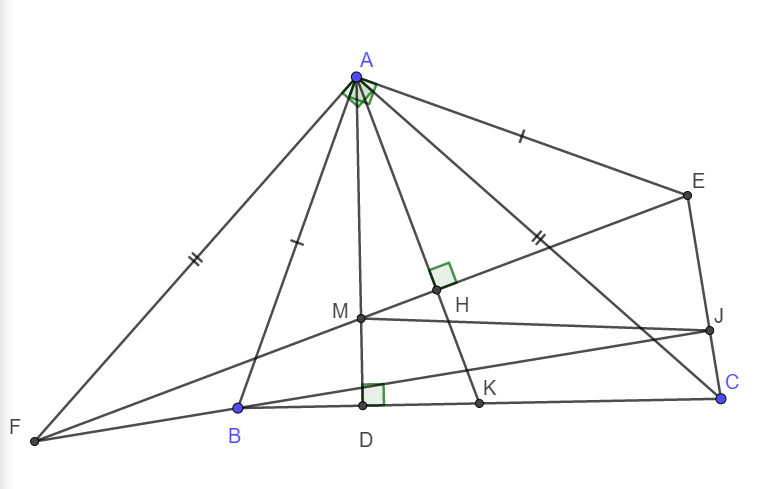
1. cho tam giác ABC. trên nửa mặt phẳng chứa đỉnh C có bờ là đường thẳng AB ta dựng đoạn thẳng AE vuông góc với AB và AE = AB. trên nửa mặt phẳng chứa đỉnh B có bờ là đường thẳng AC ta dựng đoạn thẳng AF vuông góc với AC và AF = AC. đường thẳng EF cắt đường cao AD của tam giác ABC ở M. vẽ AH vuông góc EF cắt BC ở K ( H thuộc EF )
a) tam giác ACK = tam giác FAM
b) M là trung điểm EF
c) FB vuông góc với EC và FB = EC
2. cho tam giác ABC vuông tại A. AH là đường cao. đường phân giác góc B. góc C cắt nhau tại I ; đường phân giác góc B và BAH cắt nhau tại M ; đường phân giác góc C và góc CAH cắt nhau tại N. đường thẳng MN cắt AB,AC theo thứ tự tại B' và C'
a) CM I là trực tâm tam giác AMN
b) có kết luận gì về tam giác AB'C'
a) Xét tam giác ACK và tam giác FAM có :
AC = FA
\(\widehat{CAK}=\widehat{AFM}\) (Cùng phụ với góc \(\widehat{FAK}\) )
\(\widehat{ACK}=\widehat{FAM}\) (Cùng phụ với góc \(\widehat{DAC}\) )
\(\Rightarrow\Delta ACK=\Delta FAM\left(g-c-g\right)\)
b) Do \(\Delta ACK=\Delta FAM\left(cma\right)\Rightarrow FM=AK\)
Chứng minh hoàn toàn tương tự câu a ta có: \(\Delta ABK=\Delta EAM\left(g-c-g\right)\)
\(\Rightarrow ME=AK\)
Từ đó suy ra FM = ME hay M là trung điểm EF.
c) Kéo dài FB cắt EC tại J. Ta chứng minh \(\widehat{FJE}=90^o\)
Xét tam giác FAB và tam giác CAE có:
FA = CA
AB = AE
\(\widehat{FAB}=\widehat{CAE}\) (Cùng phụ với góc \(\widehat{BAC}\) )
\(\Rightarrow\Delta FAB=\Delta CAE\left(c-g-c\right)\)
\(\Rightarrow FB=CE\) và \(\widehat{AFB}=\widehat{ACE}\)
Xét tứ giác AFJE có:
\(\widehat{AFJ}+\widehat{FJE}+\widehat{JEA}+\widehat{EAF}=360^o\)
\(\Rightarrow\widehat{ACE}+\widehat{FJE}+\widehat{CEA}+\widehat{EAC}+90^o=360^o\)
\(\Rightarrow\widehat{FJE}+\widehat{ACE}+\widehat{CEA}+\widehat{EAC}=270^o\)
\(\Rightarrow\widehat{FJE}+180^o=270^o\)
\(\Rightarrow\widehat{FJE}=90^o\)
Vậy nên \(FB\perp EC\) (đpcm).
Bài 2:
a) Gọi giao điểm của đường phân giác ^ABC và ^ACB với AC và AB lần lượt là E và D
Dễ thấy: ^BAH=^ACB (Cùng phụ với ^HAC) => 1/2. ^BAH = 1/2. ^ACB
=> ^DAM=^ACD. Mà ^DAM+^MAC=^BAC=900 => ^ACD+^MAC=900 => AM \(\perp\)CD
hay NI\(\perp\)AM.
Tương tự ta chứng minh MI\(\perp\)AN
Xét tam giác MAN: NI\(\perp\)AM; MI\(\perp\)AN => I là trực tâm của tam giác MAN (đpcm).
b) Do I là trực tâm của tam giác AMN (cmt) => AI\(\perp\)MN hay AI\(\perp\)B'C'
Ta có: Tam giác ABC có 2 đường phân giác ^ABC và ^ACB cắt nhau tại I => AI là phân giác ^BAC
=> AI là phân giác ^B'AC'.
Xét tam giác AB'C': AI là phân giác ^B'AC'. Mà AI\(\perp\)B'C' => Tam giác AB'C' cân tại A
Lại có: ^B'AC'=900 => Tam giác B'AC' vuông cân tại A.
Câu hỏi của SKT_NTT - Toán lớp 7 - Học toán với OnlineMath bài này câu c làm thế nào nhỉ
Cho tam giác ABC vuông tại A. Phân giác BF .từ I nằm giữa B và F.Vẽ đường thẳng song song AC cắt AB Ac lần lượt tại M và N .vẽ đường tròn ngoài tiếp tam giác BIN cắt đường thẳng AI tại D.các đường thẳngDN và BF cắt nhau tại E. chứng minh 5 điểm A, B,C,D,E cùng thuộc một đường tròn và BE vuông góc CE
Sửa lại đề Từ I kẻ đường thẳng song song AC cắt AB,BC lần lượt tại M,N
Vì MN//AC nên: \(\widehat{ACB}=\widehat{INB}\)(đồng vị)
Mà BIND là tứ giác nội tiếp nên: \(\widehat{ADB}=\widehat{INB}\)
Cho nên: \(\widehat{ACB}=\widehat{ADB}\)
Suy ra: ABDC là tứ giác nội tiếp
Đồng thời: \(\widehat{ADE}=\widehat{NBI}=\widehat{ABE}\Rightarrow\)ABDE là tứ giác nội tiếp
Vậy A,B,C,D,E cùng thuộc một đường tròn
Hơn nữa: tam giác ABC vuông tại A
Suy ra: BC là đường kính của đường tròn ngoại tiếp ngũ giác ABDCE
Vậy BE vuông góc CE
Hình vẽ:(Mình k chắc nó có hiện ra k nha )





Trl :
Bạn kia làm đúng rồi nhé !
Học tốt nhé bạn @