BC < 2AC nếu \(\frac{1}{2}\)BC = CD < AC

Xét hai tam giác ADC có \(\widehat{D_1}\)=\(\widehat{G_1}\)+\(\widehat{B_1}\).Theo giả thiết \(\widehat{G_1}\)=\(90^o\)nên \(\widehat{D_1}\)là góc tù. 

Cạnh AC đối diện với \(\widehat{D_1}\)nên là cạnh lớn nhất. Vậy AC > DC hay 2AC > 2DC = BC

bó tay .com.vn

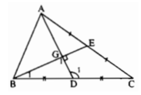
Gọi giao điểm của hai đường thẳng AD và BE là G.

+) Xét tam giác BDG có góc ∠D1 là góc ngoài tam giác nên :

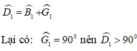
+)Xét tam giác ADC có ∠D1 + ∠A + ∠C = 180º mà ∠D1 > 90º nên ∠D1 là góc lớn nhất trong tam giác đó:

Suy ra: ∠D1 > ∠A

Suy ra: AC > CD ( cạnh đối diện với góc lớn hơn thì lớn hơn ). (1)

+) Mà D là trung điểm của BC nên 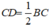 (2)

Từ (1) và (2) suy ra: 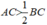 hay 2AC > BC ( điều phải chứng minh )

BC < 2AC nếu

Xét hai tam giác ADC có . Theo giả thiết nên là góc tù.

Cạnh AC đối diện với góc nên là cạnh lớn nhất, vậy AC > DC hay 2AC > 2DC = BC.

\(\text{Xét: }\Delta BGA\perp G\text{ thì }BG^2+GA^2=AB^2\)

\(\Leftrightarrow\frac{4}{9}\left(BE^2+AD^2\right)=AB^2\)

\(\Leftrightarrow BE^2+\frac{1}{4}BC^2=\frac{27}{2}\)(1)

\(\text{Có trong: }\Delta ABE\text{ thì }AB^2+AE^2\)

\(\Leftrightarrow6+\frac{1}{4}AC^2=BE^2\)(2)

Từ (1) và (2), ta có: 

\(BC^2+AC^2=30\left(cm\right)\)

Mà: \(BC^2-AC^2=AB^2=6\left(cm\right)\)

Nên \(BC^2=18\)

\(\Rightarrow BC=3\sqrt{2}\left(cm\right)\)

Áp dụng Pitago cho tg ABG

Áp dụng Pitago cho tg BDG

Tiếp tục làm tiếp nha bạn :")

Tính cách thuận tiện : 64 x 6 + 81 x 4 + 17x 6