Cho hình thang ABCD ()0AD 90==; CD = 2AB = 2AD.a)Tính số đo góc BCD, góc ABCcủa hình thang ABCD.b)Chứng minh BD vuông góc với BC.c)LấyKlà điểm tùy ý trên AB. KẻKx vuông góc với DK; Kxcắt BC tại H.Chứng minh DKHvuông cân.

Những câu hỏi liên quan
Cho hình thang ABCD có góc A= góc D=90 độ.Có AB=3cm,BC=5cm.Tính diện tích hình thang ABCD
Cho hình thang vuông ABCD ( AB//CD ) góc DAB=90 độ góc BCD =45 độ, AB=3cm, AD =4 cm
a, Tính góc B ?
b, Tính chu vi hình thang ABCD
c, Tính diện tích hình thang ABCD
Cho hình thang ABCD có A=B=90, B=60, CD=30cm, CA vuông góc CB. Tính diện tích hình thang ABCD
Tam giác ACD vuông tại C có góc CAD = góc ABC = 60 độ (cùng phụ với CAB)
=> AC = 2AD
Áp dụng Pytago ta có:
AC2 = AD2 + DC2
<=> 4AD2 = AD2 + 900
<=> AD2 = 300
<=> AD=10√3AD=103
Kẻ CH vuông với AB
AHCD là hình chữ nhật (có góc A=D=H = 900)
=> AH = CD = 30; CH = AD = 10√3103
Tgiac ACB vuông tại C, ta có:
CH2 =HA.HB
=> HB=CH2/ H A=10
=> AB = AH + HB = 40
diện tích hình thang ABCD=1/2CH.(AB+CD)=350√3
Thank ✎﹏ԍιɴɴʏ✿wᴇᴀsʟᴇʏッ ( ✎﹏ɬɛąɱ✿ɧαɾɾγρσττεɾ✔ ) nha!
Cho hình thang ABCD có góc A = góc B = 90 độ, AB=AD=3cm. Tính các góc của hình thang ABCD
Cho hình thang ABCD có góc A=D =90
AB =CD=3cm.Tinh các góc hình thang ABCD
Bốn góc hình thang ABCD đều bằng 90 độ
Đúng 100%
Chúc Nguyễn Sỹ Tuấn học tốt!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình bình hành ABCD có góc A=D,=90° và DC 2AB biết đáy nhỏ = chiều cao hình thang = 4cm , tính diện tích hình thang ABCD
1, cho hình thang vuông ABCD có A = D = 90 độ , AB = AD =2 cm , CD= 4cm . tính B , C của hình thang.
2, cho hình thangg vuông ABCD có A = D =90 độ , CD = BC =2AB . Tính góc ABC.
\(2,\)
Kẻ BH vuông góc với CD tại H
Xét hai tam giác BDH và BCH:
+) BH là cạnh chung
+) Góc BHD = góc BHC = 90 độ
+) DH = CH
=> Tam giác BDH = tam giác HCH (c.g.c)
=> BD = BC
Khác: DC = BC
=> BC = CD = DB => Tam giác BCD đều => Góc C = 60 độ
Mà: AB // CD => Góc B + góc C = 180 độ => Góc B = góc ABC = 180 độ - 60 độ = 120 độ
Cho hình thang ABCD có ABBCa, AD2a,
A
^
B
^
90
°
. Tính thể tích khối tròn xoay sinh ra khi hình thang ABCD quay quanh CD.
Đọc tiếp
Cho hình thang ABCD có AB=BC=a, AD=2a, A ^ = B ^ = 90 ° . Tính thể tích khối tròn xoay sinh ra khi hình thang ABCD quay quanh CD.
![]()
![]()
![]()
![]()
Cho hình thang ABCD có
A
^
D
^
90
°
, DC BC 2.AB, DC 4cm. Tính góc ABC của hình thang. A.
110
°
B.
150
°
C.
120
°
D.
135
°
Đọc tiếp
Cho hình thang ABCD có A ^ = D ^ = 90 ° , DC = BC = 2.AB, DC = 4cm. Tính góc ABC của hình thang.
A. 110 °
B. 150 °
C. 120 °
D. 135 °
Đáp án cần chọn là: C
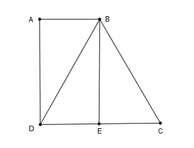
Từ B kẻ BE vuông góc với CD tại E.
Tứ giác ABED là hình thang có hai cạnh bên AD // BE nên AD = BE, AB = DE.
Mặt khác, DC = BC = 2AB nên DC = 2ED, do đó E là trung điểm của DC.
Xét ΔBDE và ΔBCE có B E D ^ = B E C ^ = 90 ° ; DE = EC
BE cạnh chung nên ΔBED = ΔBEC (c – g – c)
Suy ra BD = BC mà BC = DC (gt) => BD = BC = CD nên ΔBCD đều.
Xét ΔBCD đều có BE là đường cao cũng là đường phân giác nên
E B C ^ = 1 2 D B C ^ = 1 2 × 60 ° = 30 °
Vì AD // BE mà B A D ^ = 90 ° nên A B E ^ = 180 ° - B A D ^ = 180 ° - 90 ° = 90 ° (hai góc trong cũng phía bù nhau)
Từ đó A B C ^ = A B E ^ + E B C ^ = 90 ° + 30 ° = 120 °
Vậy A B C ^ = 120 °
Đúng 0
Bình luận (0)



















