So sánh hai luỹ thừa bằng cách tính giá trị cụ thể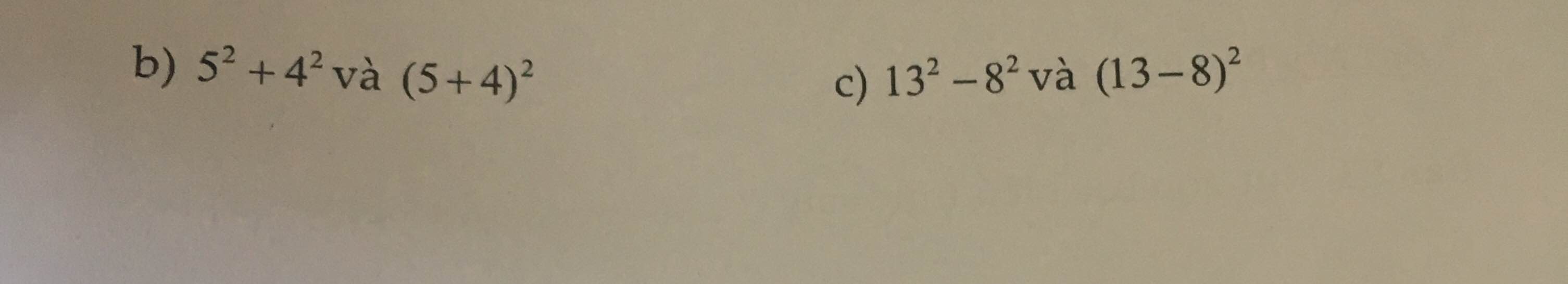

Những câu hỏi liên quan
So sánh 2 lũy thừa bằng cách tính giá trị cụ thể :
a,\(18^2\)và \(10^3\)
b,\(3^2+4^2\) và \(\left(3+4\right)^2\)
182=22.34
103=23.53.vì 3>2=>23>22
53=125 mà 34=81=> 5^3>3^4.vậy....
Đúng 0
Bình luận (0)
a, \(18^2=324\)
\(10^3=1000\)
Vì \(1000>324\Rightarrow10^3>18^2\)
b, \(3^2+4^2=9+16=25\)
\(\left(3+4\right)^2=7^2=49\)
Vì \(49>25\Rightarrow\left(3+4\right)^2>3^2+4^2\)
Đúng 0
Bình luận (0)
Không tính giá trị cụ thể, hãy so sánh hai biểu thức
\(F=2002\cdot2004=2003^2-1< 2003^2=E\)
Đúng 1
Bình luận (0)
Câu 10:so sánh với cách tính toán với cách lấy giá trị cụ thể và cách tính toán với cách lấy địa chỉ ô trong chương trình bảng tính
So sánh hai tích sau mà không tính cụ thể giá trị của chúng: A = 2019.2021 và B = 2018.2022
A = 2019.2021 = (2018+1).2021 = 2018.2021 + 2021.
B = 2018.2022 = 2018.(2021+1) = 2018.2021+2018.
Vì 2018.2021+2021 >2018.2021+2018 nên A > B.
Đúng 0
Bình luận (0)
So sánh hai tích sau mà không tính cụ thể giá trị của chúng: A = 2018.2018 và B = 2017.2019
A = 2018.2018 - 2018.(2017+1) = 2018.2017 + 2018.
B = 2017.2019 = 2017.(2018+1) = 2017.2018 + 2017.
Vì 2018.2017 + 2018 > 2017.2018 + 2017 nên A > B.
Đúng 0
Bình luận (0)
ko tính giá trị cụ thể hãy so sánh hai biểu thức : A=198.202 và B=200.200
A = 198 . 202 B = 200 . 200
A = 198 . ( 200+ 2 ) B = (198 + 2 ) . 200
A = 198 . 200 + 198 . 2 B = 198 . 200 + 2 . 200
VI 198 . 2 < 2. 200 NEN A < B
Đúng 0
Bình luận (0)
so sánh hai số A và B ma ko tính cụ thể giá trị của chúng A = 2011 . 2011 B = 2010.2012
B=2010.2012=(2011-1).(2011+1)=2011.2011-1<2011.2011=A
Không tính giá trị cụ thể , hãy so sánh ( giải 4 cách ) a) A = 1374.57+687.80 và B= 260.130+740.140 | C = 2017 .2017 và D= 2016.2016
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Đúng 0
Bình luận (0)
Không tính giá trị cụ thể, hãy so sánh hai biểu thức sau:
C=35.53-18 và D =35+53.34
Ta có :
C = 35 . 53 - 18
= ( 34 + 1 ) . 53 - 18
= 53 . 34 + 53 - 18
= 53 . 34 + 35 = D
Vậy C = D
Đúng 0
Bình luận (0)
Ta có
C = 35 . 53 - 18
C = ( 34+1 ) . 53 - 18
C = 53 .34 + 53 - 18
C = 53 . 34 + 35
Vậy ta có thể nói C = D
Đúng 0
Bình luận (0)




















