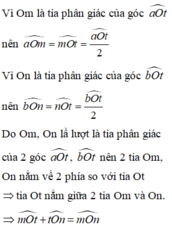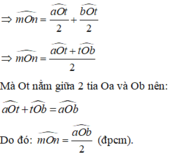cho AOB=100 và Ot là tia phân giác của góc AOB .Chứng minh rằng AxllOt và ByllOt

Những câu hỏi liên quan
Cho góc AOB 100 độ,OC là tia phân giác của góc AOB gọi OM và ON thuộc AOB sao cho AOM = BON =25 ĐỘ . Chứng minh rằng OC là phân giác của góc MON
Cho góc AOB =100 độ ,OC là tia phân giác của góc đó ,trong góc AOB vẽ các tia OD và OE sao cho góc AOD =AOE =20 độ .chứng minh rằng tia OC là tia phân giác của góc DOE
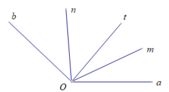
Cho góc aOb và tia Ot nằm giữa 2 tia Oa, Ob. Các tia Om, On theo thứ tự là tia phân giác của góc aOt và góc bOt . Chứng tỏ rằng m O n ^ = a O b ^ 2
cho góc aOb=100 độ, Oc là tia phân giác của góc aOb. trong góc aOb vẽ Od và Oe sao cho aOd=bOc=20 độ. chứng minh Oc là tia phân giác của góc dOe?
CHO AOB LÀ MỘT GÓC TÙ, TRONG GÓC ẤY VẼ CÁC TIA OA' VÀ OB' THEO THỨ TỰ VUÔNG GÓC VỚI OA VÀ OB. CHỨNG MINH RẰNG:
a) AOB'=A'OB
b) TIA PHÂN GIÁC A'OB' CŨNG LÀ TIA PHÂN GIÁC CỦA AOB.
c) CÁC TIA PHÂN GIÁC CỦA AOB' VÀ A'OB VUÔNG GÓC VỚI NHAU
CHO AOB LÀ MỘT GÓC TÙ, TRONG GÓC ẤY VẼ CÁC TIA OA' VÀ OB' THEO THỨ TỰ VUÔNG GÓC VỚI OA VÀ OB. CHỨNG MINH RẰNG:
a) AOB'=A'OB
b) TIA PHÂN GIÁC A'OB' CŨNG LÀ TIA PHÂN GIÁC CỦA AOB.
c) CÁC TIA PHÂN GIÁC CỦA AOB' VÀ A'OB VUÔNG GÓC VỚI NHAU
Cho góc aOb và tia Ot nằm giữa Oa , Ob . Các tia Om,On thứ tự là tia phân giác của góc aOt và bOt . Chứng tỏ rằng \(\widehat{mOn}=\frac{\widehat{aOb}}{2}.\)
ta có \(Om\) là phân giác của \(\widehat{aOt}\) => \(\widehat{mOt}=\frac{\widehat{aOt}}{2}\)
tương tự ta có \(\widehat{nOt}=\widehat{\frac{bOt}{2}}\)
=> \(\widehat{mOt}+\widehat{nOt}=\frac{\widehat{aOt}+\widehat{bOt}}{2}=\widehat{\frac{aOb}{2}}\)
mà \(Ot\) nằm giữa \(Om\) và \(On\)
=> \(\widehat{mOn}=\widehat{mOt}+\widehat{nOt}=\widehat{\frac{aOb}{2}}\) (ĐPCM)
Đúng 0
Bình luận (0)
Cho góc tù AOB. Trong góc ấy vẽ các tia OA' vàOB' theo thứ tự vuông góc với OA và OB. Chứng minh rằng:
a) góc AOB' = góc A'OB
b) tia phân giác của góc A'OB' cũng là tia phân giác của góc AOB
c) các tia phân giác của góc AOB' và A'OB vuông góc với nhau
cho hai góc kề bù aob và bot. gọi om là tia phân giác của aob. trong góc bot, vẽ tia on vuông góc với om ,chứng minh rằng: on là tia phân giác của bot
Ta có: Om là phân giác của góc aOb
=>\(\widehat{aOm}=\widehat{bOm}=\dfrac{1}{2}\cdot\widehat{aOb}\)
Ta có: Ob nằm giữa hai tia Om và On
=>\(\widehat{mOb}+\widehat{nOb}=\widehat{mOn}\)
=>\(\widehat{nOb}=\widehat{mOn}-\widehat{mOb}\)
Ta có: \(\widehat{aOb}+\widehat{bOt}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{bOm}+\widehat{bOt}=2\cdot90^0=2\cdot\widehat{mOn}\)
=>\(\widehat{bOt}=2\left(\widehat{mOn}-\widehat{bOm}\right)=2\cdot\widehat{bOn}\)
=>On là phân giác của góc bOt
Đúng 1
Bình luận (0)