Tìm M trên Oy biết rằng M cách đều hai điểm A (1, 2, -1) và B (-2, 0, 5)

Những câu hỏi liên quan
1. Tìm M trên Oy biết rằng M cách đều hai điểm A (1, 2, -1) và B (-2, 0, 5)
2. Tính độ dài đường cao OH của tam giác OAB với A (0, 1, -2) và B (2, 1, 3)
Cho góc xOy khác góc bẹt , điểm A thuộc cạnh Ox , điểm B thuộc cạnh Oy .
a) Hãy tìm điểm M nằm trong góc xOy, cách đều Ox , Oy và cách đều A , B.
b) Nếu OA=OB thì có bao nhiêu điểm M thoả mãn các điều kiện trong câu a ?
Hai điểm A và B trên cùng một bán kính của một vôlăng đang quay đều, cách nhau 20 cm. Điểm A ở phía ngoài có vận tốc
v
A
0,6 m/s, còn điểm B có
v
B
0,2 m/s. Tốc độ góc của vôlăng và khoảng cách từ điểm B đến trục quay là A. 2 rad/s ; 10 cm B. 3 rad/s ; 30 cm C. 1 rad/s ; 20 cm D. 4 rad/s ; 40 cm
Đọc tiếp
Hai điểm A và B trên cùng một bán kính của một vôlăng đang quay đều, cách nhau 20 cm. Điểm A ở phía ngoài có vận tốc v A = 0,6 m/s, còn điểm B có v B = 0,2 m/s. Tốc độ góc của vôlăng và khoảng cách từ điểm B đến trục quay là
A. 2 rad/s ; 10 cm
B. 3 rad/s ; 30 cm
C. 1 rad/s ; 20 cm
D. 4 rad/s ; 40 cm
Chọn A.
Hai điểm A và B quay cùng tốc độ góc nên ta có:
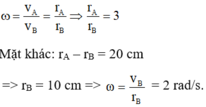
Đúng 0
Bình luận (0)
Hai điểm A và B trên cùng một bán kính của một vôlăng đang quay đều, cách nhau 20 cm. Điểm A ở phía ngoài có vận tốc
v
A
0
,
6
m
/
s
, còn điểm B có
v
B
0
,
2
m
/
s
. Tốc độ góc của vôlăng và khoảng cách từ điểm B đến trục quay là A. 2 rad/s ; 10 cm. B. 3 rad/s ; 30 cm....
Đọc tiếp
Hai điểm A và B trên cùng một bán kính của một vôlăng đang quay đều, cách nhau 20 cm. Điểm A ở phía ngoài có vận tốc v A = 0 , 6 m / s , còn điểm B có v B = 0 , 2 m / s . Tốc độ góc của vôlăng và khoảng cách từ điểm B đến trục quay là
A. 2 rad/s ; 10 cm.
B. 3 rad/s ; 30 cm.
C. 1 rad/s ; 20 cm.
D. 4 rad/s ; 40 cm.
Chọn A.
Hai điểm A và B quay cùng tốc độ góc nên ta có:
![]()
Mặt khác: rA – rB = 20 cm => rB = 10 cm
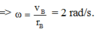
Đúng 0
Bình luận (0)
Cho hàm số y m.x + 3 – 2n (d). Tìm m và n biết:
a) (d) đi qua điểm A( 1, 2) và song song với đường thẳng y 2.x + 4. Vẽ đường thẳng với m và n tìm được.
b) (d) đi qua hai điểm M( -2 ; 3) và N( 2 ; 4).
c) (d) đi qua gốc tọa độ và vuông góc với đường thẳng y 3.x – 1.
d) (d) song song với đường thẳng y 5.x + 1 và đi qua giao điểm của hai đường thẳng y x + 1 và y 3.x + 5.
Đọc tiếp
Cho hàm số y = m.x + 3 – 2n (d). Tìm m và n biết:
a) (d) đi qua điểm A( 1, 2) và song song với đường thẳng y = 2.x + 4. Vẽ đường thẳng với m và n tìm được.
b) (d) đi qua hai điểm M( -2 ; 3) và N( 2 ; 4).
c) (d) đi qua gốc tọa độ và vuông góc với đường thẳng y = 3.x – 1.
d) (d) song song với đường thẳng y = 5.x + 1 và đi qua giao điểm của hai đường thẳng y = x + 1 và y = 3.x + 5.
a: Vì (d)//y=2x+4 nên m=2
Vậy: (d): y=2x+3-2n
Thay x=1 và y=2 vào (d), ta được:
5-2n=2
hay n=3/2
Đúng 1
Bình luận (0)
1. Cho 3 điểm A; B; C bất kì và một điểm O khác với các điểm A; B; C. Hỏi có bao nhiêu tia gốc O và đi qua một trong 3 điểm A; B; C
2. Trên một đường thẳng lấy 4 điểm M; N; P; Q : Biết rằng điểm P nằm giữa 2 điểm N và Q và điểm N nằm giữa 2 điểm M và P. CMR : N nằm giưã M và Q
Trên đường thẳng d lấy bốn điểm A, B, M, N sao cho điểm M nằm giữa hai điểm A, N và điểm N nằm giữa hai điểm B, M. Biết rằng AB = 10cm, NB = 2cm và AM = BN. Tính độ dài của đoạn thẳng MN.
Theo giả thiết ta vẽ được hình:

Khi đó AN = AM + MN và AB = AN + NB.
Suy ra AB = (AM + MN) + NB
Do AM = NB = 2 cm nên 10 = 2 + MN + 2.
Từ đó tính được MN = 10 - 4 = 6 (cm)
Đúng 0
Bình luận (0)
2 bến sông A và B cách nhau 16km.Cùng 1 lúc cano 1 đĩuôi dòng từ A đến B và cano 2 đi ngược dòng từ B về A.Hỏi sau bao lâu 2 cano gặp nhau biết rằng vận tốc của hai cano khi nước lặng đều bằng 16 km/h và vận tốc dòng nước là 2km/h
cho tam giác abc nội tiếp đường tròn tâm O bán kính R. M là 1 điểm tùy ý trên đáy BC( M khác B, C) . Vẽ đường tròn O1 đi qua M và tiếp xúc với AB tại B. Vẽ đường tròn tâm O2 qua M và tiếp xúc với AC tại C. Hai đường tròn (O1) và (O2) cắt nhau tại điểm thứ hai D1) chứng minh D nằm trên đường tròn2) Chứng minh rằng khi M thay đổi trên đáy Bc thì các đường thẳng MD luôn đi qua 1 điểm cố định3) giả sử tam giác ABC đều. Tính tích AM.AD theo R....
Đọc tiếp
cho tam giác abc nội tiếp đường tròn tâm O bán kính R. M là 1 điểm tùy ý trên đáy BC( M khác B, C) . Vẽ đường tròn O1 đi qua M và tiếp xúc với AB tại B. Vẽ đường tròn tâm O2 qua M và tiếp xúc với AC tại C. Hai đường tròn (O1) và (O2) cắt nhau tại điểm thứ hai D
1) chứng minh D nằm trên đường tròn
2) Chứng minh rằng khi M thay đổi trên đáy Bc thì các đường thẳng MD luôn đi qua 1 điểm cố định
3) giả sử tam giác ABC đều. Tính tích AM.AD theo R. Em có nhân xét gì qua kết quả vừa tìm được.













