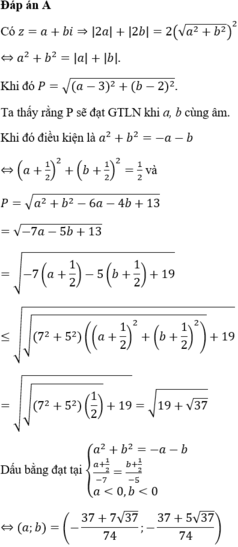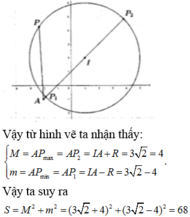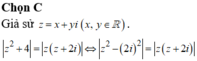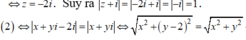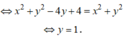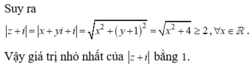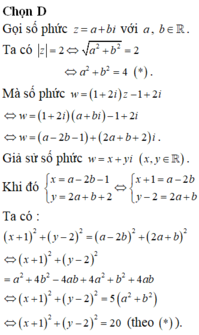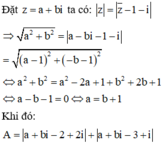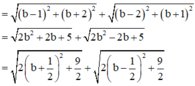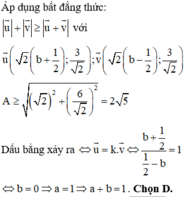Cho số phức z thoả mãn điều kiện |z4 +4 | = | z(z+2i) |. Tính giá trị nhỏ nhất của |z+i|

Những câu hỏi liên quan
Cho số phức z thoả mãn điều kiện |z+
z
|+|z-
z
|2|
z
2
|. Tìm giá trị lớn nhất của biểu thức P|z-3-2i|. A.
19
+
37
B.
37
+
19
C.
2
+
5
D.
5
+
2
Đọc tiếp
Cho số phức z thoả mãn điều kiện |z+ z |+|z- z |=2| z 2 |. Tìm giá trị lớn nhất của biểu thức P=|z-3-2i|.
A. 19 + 37
B. 37 + 19
C. 2 + 5
D. 5 + 2
Cho số phức z thỏa mãn điều kiện
z
-
1
-
2
i
4
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
z
+
2
+
i
Tính giá trị của tổng SM2+ m2 A. S 82 B. . S 34 C. S 68 D. S 36.
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z - 1 - 2 i = 4 Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z + 2 + i Tính giá trị của tổng S=M2+ m2
A. S = 82
B. . S = 34
C. S = 68
D. S = 36.
Cho số phức z thỏa mãn điều kiện |z -2 + 2i | + | z + 1 -3i |
34
. Hãy tìm giá trị lớn nhất, giá trị nhỏ nhất của |z + 1 + i|. A.
6
34
v
à
8
B.
6
34
17
v
à
4
C.
34...
Đọc tiếp
Cho số phức z thỏa mãn điều kiện |z -2 + 2i | + | z + 1 -3i | = 34 . Hãy tìm giá trị lớn nhất, giá trị nhỏ nhất của |z + 1 + i|.
A. 6 34 v à 8
B. 6 34 17 v à 4
C. 34 v à 8
D. Đáp án khác.
Chọn B.
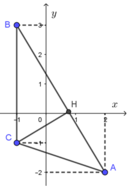
Gọi M (x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.
Gọi điểm A(2; -2) ; B(-1; 3) và C(-1; -1)
Phương trình đường thẳng AB: 5x + 3y - 4 = 0.
Khi đó theo đề bài ![]()
Ta có ![]() . Do đó quỹ tích M là đoạn thẳng AB.
. Do đó quỹ tích M là đoạn thẳng AB.
Tính CB = 4 và ![]() .
.
Hình chiếu H của C trên đường thẳng AB nằm trên đoạn AB.
Vậy 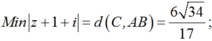
![]()
Đúng 0
Bình luận (0)
Cho số phức z thoả mãn |z – 1 + 3i| + |z + 2 – i| = 8. Tìm giá trị lớn nhất, giá trị nhỏ nhất của P = |2z + 1 = 2i|.
A. 8 và 4
![]()
![]()
![]()
Chọn D.
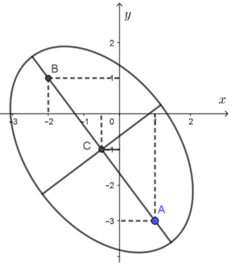
Ta có P = |2z + 1 = 2i| nên 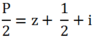
Ta cần tìm giá trị lớn nhất, giá trị nhỏ nhất của: 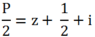
Ta có z1 = 1 - 3i; z2 = -2 + i và z0 = -1/2 - i
Ta thấy: ![]()
Tính 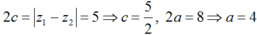
Suy ra 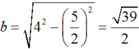
Vậy Max P = 2.4 = 8 và 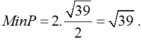
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn điều kiện
z
-
3
+
2
i
z
-
i
Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z - 3 + 2 i = z - i Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
![]()
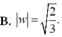
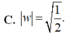
![]()
Cho số phức z thỏa điều kiện
z
2
+
4
z
z
+
2
i
. Giá trị nhỏ nhất của
z
+
i
bằng ? A. 3 B. 4 C. 1 D. 2
Đọc tiếp
Cho số phức z thỏa điều kiện z 2 + 4 = z z + 2 i . Giá trị nhỏ nhất của z + i bằng ?
A. 3
B. 4
C. 1
D. 2
Cho các số phức z thoả mãn
z
2
. Đặt
w
(
1
+
2
i
)
z
-
1
+
2
i
. Tìm giá trị nhỏ nhất của
w
A. 2 B.
3
5
C.
2
5
D.
5
Đọc tiếp
Cho các số phức z thoả mãn z = 2 . Đặt w = ( 1 + 2 i ) z - 1 + 2 i . Tìm giá trị nhỏ nhất của w
A. 2
B. 3 5
C. 2 5
D. 5
Cho số phức
z
a
+
bi
(
a
,
b
∈
ℕ
)
thỏa mãn đồng thời hai điều kiện
|
z
|
|
z
-
1...
Đọc tiếp
Cho số phức z = a + bi ( a , b ∈ ℕ ) thỏa mãn đồng thời hai điều kiện | z | = | z - 1 - i | và biểu thức A = | z - 2 + 2 i | + | z - 3 + i | đạt giá trị nhỏ nhất. Giá trị của biểu thức a + b bằng
A. -1.
B. 2.
C. -2.
D. 1.
Cho số phức
z
a
+
b
i
a
,
b
∈
ℝ
thỏa mãn đồng thời hai điều kiện
z
z
¯
-
1
-
i
và biểu thức
A
z
-...
Đọc tiếp
Cho số phức z = a + b i a , b ∈ ℝ thỏa mãn đồng thời hai điều kiện z = z ¯ - 1 - i và biểu thức A = z - 2 + 2 i + z - 3 + i đạt giá trị nhỏ nhất. Giá trị của biểu thức a+b bằng
A. -1
B. 2
C. -2
D. 1