Cho tam giác ABC cân tại A. Kẻ AD vuông góc với BC. Chứng minh rằng AD là tia phân giác của góc A ?

Những câu hỏi liên quan
Cho tam giác cân tại A. Kẻ AD vuông góc với BC. Chứng minh rằng AD là tia phân giác của góc A
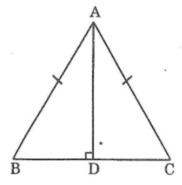
Xét hai tam giác vuông ADB và ADC, ta có:
∠(ADB) =∠(ADC) = 90o
AB = AC (giả thiết)
AD cạnh chung
Suy ra: ΔADB= ΔADC(cạnh huyền, cạnh góc vuông)
⇒ ∠(BAD) =∠(CAD) (hai góc tương ứng)
Vậy AD là tia phân giác ∠(BAC)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Từ A kẻ AH vuông góc với BC tại H, tia phân giác của góc CAH cắt BC. Chứng minh rằng:
a) Tam giác ABD cân
b) Các tia phân giác của góc BAH và BHA cắt nhau tại I. Gọi M là trung điểm của AD. Chứng minh B, I, M thẳng hàng
c) Gọi N trung điểm của BC. Chứng minh 2AN = BC
d) A Chứng minh AB + AC = 2AM
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H. Kẻ tia phân giác AD của góc BAH tại D.
a) Chứng minh rằng : Góc BAH = góc C , góc CAH = góc B
b) Chứng minh rằng : Góc DAC = góc ADC
c) Kẻ tia phân giác của góc C cắt AD tại K. Chứng minh rằng CK vuông góc với AD .
Bạn tham khảo ở đây:
Câu hỏi của ngô thị gia linh - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Ai giúp bạn này với, tiện thể giúp luôn cả mình nhé. Cô Trần THị Loan ơi giúp bọn em ạ
Đúng 0
Bình luận (0)
Cho ABC cân tại A. kẻ AD vuông góc với BC. Chứng minh AD là tia phân giác của góc A.
xét 2 tam giác vuông BAD và CAD có :AD : cạnh chungAB = AC ( vì tam giác ABC cân tại A )=> tam giác BAD = tam giác CAD ( cạnh huyền - cạnh góc vuông)=> ^BAD = ^CAD ( 2 góc tương ứng )=> AD là tia phân giác của góc A
Đúng 1
Bình luận (1)
Cho tam giác ABC cân tại BC can tai A và AD là phân giác của góc BAC . Từ D kẻ DE vuông góc với AB và DF vuông góc với AC a) Chứng Minh Rằng AD là đường trung trực của BC
Xét tam giác ABC cân tại A có:
AD là phân giác của góc BAC (gt).
\(\Rightarrow\) AD là đường trung trực của BC (Tính chất tam giác cân).
Đúng 1
Bình luận (0)
Cho tam giác ABC cân A . Kẻ AD vuông góc với BC . Chứng minh AD là tia phân giác góc A
Xét tam giác ABD vuông tại D và tam giác ACD vuông tại D có:
AB = AC (tam giác ABC cân tại A)
B = C (tam giác ABC cân tại A)
=> Tam giác ABD = Tam giác ACD (cạnh huyền - góc nhọn)
=> BAD = CAD (2 góc tương ứng)
=> AD là tia phân giác của A
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Tia phân giác của góc B cách AC tại D. Từ D kẻ DH vuông góc với BC (H€BC) và DH cách AB tại K a) Chứng minh AD =DH b) So sánh độ dài cạnh AD và BC c) Chứng minh tam giác KBC là tam giác cân
giúp mình với. Mình cần gấp lắm :
Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt cạnh AC tại D. Qua D kẻ thẳng vuông góc với BC tại E và cắt AB tại F.
a. Chứng mình rằng : AD = ED
b. Chứng minh tam giác FBC là tam giác cân
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
\(\widehat{EBF}\) chung
Do đó: ΔBEF=ΔBAC
Suy ra: BF=BC
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A và AB <AC. Tia phân giác của góc ABC cắt cạnh AC tại D. Kẻ DE vuông góc với BC (điểm E thuộc BC).
a) Chứng minh rằng: Hai tam giác ABD và EBD bằng nhau;
b) Giải thích vì sao tam giác ADE là tam giác cân?
c) Chứng minh: 2.AD>AE;
d) Tia ED cắt tia BA tại F. Chứng minh: BD vuông góc với CF
a) Xét ABD và EBD có
BD cạnh chung
BAD=BED(=90)
ABD=EBD(vì BD là tia phân giác của B)
b ko biet
Đúng 2
Bình luận (0)
c) vì theo ý b) ADE là tam giác cân tại D nên theo py-ta-go AD+DE=AE
Nên AE>AD
(sai đầu bài rồi)
Đúng 1
Bình luận (0)
b)Vì theo ý a) BAD=BED và BD là tia phân giác của B. Nên ADE là tam giác cân
Đúng 1
Bình luận (0)





















