Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC.
Chứng minh rằng \(\widehat{BAC}=90^0\)
Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng góc BAC = 90
Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng BAC = 90 độ.
Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng ∠(BAC) = 90 độ
Vì AM là đường trung tuyến của ΔABC nên BM = MC = 1/2 BC
Mà AM = 1/2 BC (gt) nên: AM = BM = MC.
Tam giác AMB có AM = MB nên ΔAMB cân tại M
Suy ra: ∠B = ∠A1 (tính chất tam giác cân) (1)
Tam giác AMC có AM = MC nên ΔAMC cân tại M
Suy ra: ∠C = ∠A2 (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: ∠B + ∠C = ∠A1 + ∠A2 = ∠(BAC) (3)
Trong ΔABC ta có:
∠B + ∠C + ∠(BAC) = 180o (tổng ba góc trong tam giác) (4)
Từ (3) và (4) suy ra: ∠(BAC) + ∠(BAC) = 180o ⇔ 2∠(BAC) = 180o
Hay ∠(BAC) = 90o.
AM là trung tuyến
=> CM = MB = 1/2BC
AM = 1 nửa BC => AM = 1/BC
=> AM = CM = BM
=> tam giác CMA cân tại M và tam giác AMB cân tại M
=> góc C = (180 - góc CMA) : 2 và góc B = (180 - góc AMB) : 2 (tc)
=> góc C + góc B = \(\frac{180-\widehat{CMA}}{2}+\frac{180-\widehat{AMB}}{2}=\frac{180+180-\left(CMA+AMB\right)}{2}\)
\(=\frac{360-180}{2}=90\)
Xét tổng 3 góc
Xét \(\Delta\)ABC có
AM là đường trung tuyến ứng với cạnh BC và bằng nửa cạnh BC
\(\Rightarrow\Delta ABC\)vuông tại A
\(\Rightarrow\)góc BAC = \(^{90^o}\)
Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC .Chứng minh rằng góc BAC = 90 độ
Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng góc BAC = 90 độ
Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng ∠(BAC) = 90o
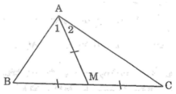
Vì AM là đường trung tuyến của ΔABC nên BM = MC = 1/2 BC
Mà AM = 1/2 BC (gt) nên: AM = BM = MC.
Tam giác AMB có AM = MB nên ΔAMB cân tại M
Suy ra: ∠B = ∠A1 (tính chất tam giác cân) (1)
Tam giác AMC có AM = MC nên ΔAMC cân tại M
Suy ra: ∠C = ∠A2 (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: ∠B + ∠C = ∠A1 + ∠A2 = ∠(BAC) (3)
Trong ΔABC ta có:
∠B + ∠C + ∠(BAC) = 180o (tổng ba góc trong tam giác) (4)
Từ (3) và (4) suy ra: ∠(BAC) + ∠(BAC) = 180o ⇔ 2∠(BAC) = 180o
Hay ∠(BAC) = 90o.
Vậy ΔABC vuông tại A.
Tam giác ABC có đường trung tuyến AM bàng nửa cạnh BC. Chứng minh rằng góc BAC = 90độ
ta có AM=1/2BC,mà BM=CM=1/2BC
=> AM=BM=CM
ta có BM=AM=> tam giác AMB cân tại M=> góc A1= góc B
ta có AM=MC=>tam giác AMC cân tại M=> góc A2=góc C
tam giác ABC có góc B+A1+A2+C=180 độ
=> A1+A1+A2+A2=180 độ
=> 2(A1+A2)=180 độ
=> A1+A2=90độ
vậy góc BAC=90 độ
giải: vò MA = MB (gt)
=> tam giác AMB cân tại M
=> góc B = góc A1 ( đ/lý) (1)
MA = MC (gt)
=> tam giác AMC cân tại M
=> góc C = góc A2 (đ/lý) (2)
trong tam giác ABC có: góc A + góc B + góc C = 1800 (đ/lý)
hay góc A1 + A2 + góc B + góc C = 1800 (3)
từ (1), (2) , (3) => 2 góc A1 + 2 góc A2 = 1800
2 ( góc A1 + góc A2) = 1800
góc A1 + góc A2 = 900
hay góc BAC = 900
1) Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD=MA.
a)Tính số đo góc ABD?
b)Chứng minh : Tam giác ABC = Tam giác BAD.
c) So sánh AM và BC.
2) Cho tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. CMR: góc BAC = 90 độ.
Chứng minh rằng: Nếu tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC thì tam giác đo vuông tại A.
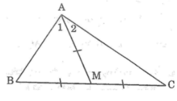
Vì AM là đường trung tuyến của ΔABC nên BM = MC = 1/2 BC
Mà AM = 1/2 BC (gt) nên: AM = BM = MC.
Tam giác AMB có AM = MB nên ΔAMB cân tại M
Suy ra: ∠B = ∠A1 (tính chất tam giác cân) (1)
Tam giác AMC có AM = MC nên ΔAMC cân tại M
Suy ra: ∠C = ∠A2 (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: ∠B + ∠C = ∠A1 + ∠A2 = ∠(BAC) (3)
Trong ΔABC ta có:
∠B + ∠C + ∠(BAC) = 180o (tổng ba góc trong tam giác) (4)
Từ (3) và (4) suy ra: ∠(BAC) + ∠(BAC) = 180o ⇔ 2∠(BAC) = 180o
Hay ∠(BAC) = 90o.
Vậy ΔABC vuông tại A.