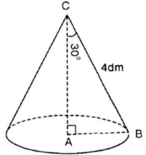
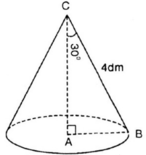
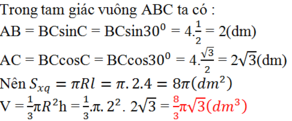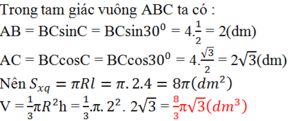Khi quay tam giác ABC vuông ở A một vòng quanh cạnh góc vuông AC cố định, ta được một hình nón. Biết \(BC=4cm,\widehat{ACB}=30^0\). Tính diện tích xung quanh và thể tích hình nón ?

Những câu hỏi liên quan
Khi quay tam giác ABC vuông ở A một vòng quanh cạnh góc vuông AC cố định, ta được một hình nón. Biết rằng BC = 4dm, góc A C B = 30 ° . Tính diện tích xung quanh và thể tích hình nón.
Khi quay tam giác ABC vuông ở A một vòng quanh cạnh góc vuông AC cố định, ta được một hình nón. Biết rằng BC = 4dm, góc A C B = 30 o . Tính diện tích xung quanh và thể tích hình nón.
Khi quay tam giác ABC vuông ở A một vòng quanh cạnh góc vuông AC cố định , ta được một hình nón . Biết rằng BC = 4dm , góc ACB = 30độ . Tính diện tích xung quanh và thể tích hình nón
Khi quay tam giác ABC vuông tại A một vòng quanh cạnh góc vuông AC, được một hình nón. Biết rằng ∠(ABC) = 60 0 , BC = 8 cm.Tính diện tích xung quanh và thể tích của hình nón đó.
Xét tam giác ABC vuông tại A có: (ABC) = 60 0 , BC = 8 cm
⇒ AB = BC.cos (ABC) = 8.cos 60 0 = 4 (cm)
AC = BC.sin (ABC) = 8.sin 60 0 = 4 3 (cm)
Diện tích xung quanh của hình nón là
S x q = πrl = π.AB.BC = π.4.8 = 32 ( c m 2 )
Thể tích hình nón là:
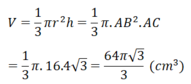
Đúng 0
Bình luận (0)
Quay tam giác vuông ABC ∠ A = 90 ° một vòng quanh cạnh AB là được một hình nón. Tính thể tích và diện tích xung quanh của hình nón đó biết BC = 12cm và ABC = 30 ° .
Quay Tam giác DEF vuông tại D một vòng quanh cạnh DE cố định ta được hình nón tính diện tích xung quanh , diện tích toàn phần và thể tích hình nón EF = 6 cm ; góc DFC = 60 độ
Cho tam giác ABC vuông tại A có AB = 6 cm, BC = 10 cm . Quay một vòng quanh cạnh AB cố định ta được một hình nón có diện tích xung quanh là??
Quay tam giác \(ABC\) quanh cạnh \(AB\) cố định thu được hình nón có đỉnh là \(B\) đáy là đường tròn đáy bán kính \(AC\).
Theo định lí Pythagore ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
Diện tích xung quanh hình nón là :
\(S_{xq}=\pi rl=\pi.AC.BC=80\pi\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có
B
C
2
a
v
à
A
B
C
⏜
30
∘
. Quay tam giác vuông này quanh cạnh AB, ta được một hình nón đỉnh B. Gọi
S
1
là diện tích xung quanh của hình nón đó và
S
2
là diện tích mặ...
Đọc tiếp
Cho tam giác ABC vuông tại A có B C = 2 a v à A B C ⏜ = 30 ∘ . Quay tam giác vuông này quanh cạnh AB, ta được một hình nón đỉnh B. Gọi S 1 là diện tích xung quanh của hình nón đó và S 2 là diện tích mặt cầu có đường kính AB. Khi đó, tỉ số S 1 S 2 là
A. S 1 S 2 = 1
B. S 1 S 2 = 2 3
C. S 1 S 2 = 1 2
D. S 1 S 2 = 3 2
Đáp án B
Tam giác ABC vuông tại A có:
sin A B C ⏜ = A C B C ⇒ A C = sin 30 ∘ .2 a = a c os A B C ⏜ = A C B C ⇒ A B = c os 30 ∘ .2 a = a 3 .
Quay Δ A B C quanh trục AB ta được hình nón có bán kính đáy r = A C = a .
=> Diện tích xung quanh hình nón trên là S 1 = π r l = π . a .2 a = 2 π a 2 . Và diện tích mặt cầu đường kính AB là: S 2 = 4 π R 2 = 4 π a 3 2 2 = 3 π a 2 ⇒ S 1 S 2 = 2 π a 2 3 π a 2 = 2 3 .
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại B có
A
C
2
a
,
B
C
a
,
khi quay tam giác ABC quay quanh cạnh góc vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng A.
3
π
a
2
B.
2
π
a
2
C.
4
π
a...
Đọc tiếp
Cho tam giác ABC vuông tại B có A C = 2 a , B C = a , khi quay tam giác ABC quay quanh cạnh góc vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng
A. 3 π a 2
B. 2 π a 2
C. 4 π a 2
D. π a 2
Đáp án B
Hình nón có chiều cao AB và bán kính BC. Diện tích xung quanh của hình nón là S = π a .2 a = 2 π a 2
Đúng 0
Bình luận (0)