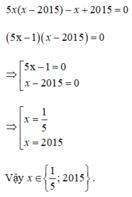\(x\left(x-2015\right)+\left(x-2015\right)=0\)

\(\Rightarrow\left(x+1\right)\left(x-2015\right)=0\)

\(\Rightarrow\hept{\begin{cases}x+1=0\\x-2015=0\end{cases}}\Rightarrow\hept{\begin{cases}x=-1\\x=2015\end{cases}}\)

\(x\left(x-2015\right)+x-2015=0\)

\(x\left(x-2015\right)+\left(x-2015\right)=\left(x-2015\right)\left(x+1\right)=0\)

TH1 :\(x+1=0\)

\(x=-1\)

TH2 : \(x-2015=0\)

\(x=2015\)

(x-2015)^x+1 - (x-2015)^x+2015

=>x-2015= 0;1;-1

x-2015=0 =>x=2015

x-2015=1 =>x=2016

x-2015=-1 =>x=2014

\(x.\left(x-2015\right)-\left(x-2015\right)=0\)

\(\left(x-1\right)\left(x-2015\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x-1=0\\x-2015=0\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=1\\x=2015\end{cases}}\)

\(x\cdot\left(x-2015\right)-x+2015=0\)

\(x\cdot\left(x-2015\right)-\left(x-2015\right)=0\)

\(\left(x-2015\right)\cdot\left(x-1\right)=0\)

\(\orbr{\begin{cases}x-2015=0\\x-1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=2015\\x=1\end{cases}}}\)

Ta có : x( x - 2015 ) - x + 2015 = 0

\(\Rightarrow\)x( x - 2015 ) - ( x - 2015 ) = 0

\(\Rightarrow\)( x - 2015 )( x - 1 ) = 0

\(\Leftrightarrow\)x - 2015 = 0 hoặc x - 1 = 0

\(\Rightarrow\)x = 2015 hoặc x = 1

Vậy : x = 2015 hoặc x = 1

Ta có: \(8x\left(x-2015\right)-x+2015=0\)

\(\Rightarrow8x\left(x-2015\right)-\left(x-2015\right)=0\)

\(\Rightarrow\left(8x-1\right)\left(x-2015\right)=0\)

\(\Rightarrow\orbr{\begin{cases}8x-1=0\\x-2015=0\end{cases}\Rightarrow\orbr{\begin{cases}x=\frac{1}{8}\\x=2015\end{cases}}}\)

Vậy \(x=\left\{\frac{1}{8};2015\right\}\)

       8x(x - 2015) - (x - 2015) = 0

<=> (8x - 1)(x - 2015) = 0

<=> ...........  đến đây thì dễ rồi :)))) 

8x(x-2015)-x+2015=0

8x(x-2015)-(x-2015)=0

(8x-1)(x-2015)=0

\(\orbr{\begin{cases}8x-1=0\\x-2015=0\end{cases}}\)=>\(\orbr{\begin{cases}8x=-1\\x=2015\end{cases}}\)=>\(\orbr{\begin{cases}x=\frac{1}{8}\\x=2015\end{cases}}\)

vậy x \(\in\){\(\frac{1}{8}\);2015}

a,|2x+2014| lớn hơn hoặc bằng 0

   |x+2015| lớn hơn hoặc bằng 0

mà |2x+2014|+|x+2015|=0

=> |2x+2014|=0

       x=-1007

|x+2015|=0

  x=-2015 (vô lí)

=> x thuộc tập hp rỗng

\(x\left(x-2015\right)-\left(x-2015\right)=0\)

\(\left(x-1\right)\left(x-2015\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x-1=0\\x-2015=0\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=1\\x=2015\end{cases}}\)

2105 mà bạn

V xl nha ^^

\(S=2015\left(\frac{1}{x}+x\right)+\left(\frac{1}{2015y}+2015y\right)-2015\left(x+y\right)\)

\(\ge2015.2\sqrt{\frac{1}{x}.x}+2\sqrt{\frac{1}{2015y}.2015y}-2015.\frac{2016}{2015}\)

\(=2.2015+2-2016=2016\)

Đẳng thức xảy ra khi x = 1; y = 1/2015.