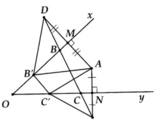
Cho A ở trong góc xOy. Tìm B thuộc Ox, C thuộc Oy sao cho chu vi tam giác ABC min.

Những câu hỏi liên quan
Cho điểm A thuộc góc xOy nhọn. Tìm B thuộc Ox, C thuộc Oy sao cho chu vi tam giác ABC nhỏ nhất.
Cho điểm A nằm trong góc nhọn xOy.
a) Tìm hai điểm M, N thuộc Ox và Oy sao cho AM + AN là nhỏ nhất.
b) Tìm hai điểm B, C thuộc Ox và Oy sao cho tam giác ABC có chu vi nhỏ nhất
cho góc xoy khác góc bẹt và A trong xoy. dựng b thuộc ox c thuộc oy
tìm điểm b và c sao cho chu vi tam giác abc đạt GTNN
cho góc xoy khác góc bẹt và A trong xoy. dựng b thuộc ox c thuộc oy
tìm điểm b và c sao cho chu vi tam giác abc đạt GTNN
Cho điểm A nằm trong góc nhọn xOy. Tìm điểm B thuộc tia Ox, điểm C thuộc tia Oy sao cho tam giác ABC có chu vi nhỏ nhất.
Cho góc nhọn xOy, điểm A nằm trong góc đó.
Dựng điểm B thuộc tia Ox, điểm C thuộc tia Oy sao cho tam giác ABC có chu vi nhỏ nhất.
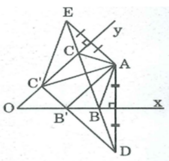
Cách dựng:
- Dựng điểm D đối xứng với A qua Ox
- Dựng điểm E đối xứng với A qua Oy
Nối DE cắt Ox tại B, Oy tại C
Tam giác ABC là tam giác có chu vi nhỏ nhất
Vì ∠ (xOy) < 90 0 nên DE luôn cắt Ox và Oy do đó ∆ ABC luôn dựng được.
Chứng minh:
Chu vi ∆ ABC bằng AB + BC + AC
Vì D đối xứng với A qua Ox nên Ox là trung trực của AD
⇒ AB = BD (tính chất đường trung trực)
E đối xứng với A qua Oy nên Oy là trung trực của AE
⇒ AC = CE (tính chất đường trung trực)
Suy ra: AB + BC + AC = BD + BC + BE = DE (1)
Lấy B' bất kì trên Ox, C' bất kì trên tia Oy. Nối C'E, C'A, B'A, B'D.
Ta có: B'A = B'D và C'A = C'E (tính chất đường trung trực)
Chu vi ∆ AB'C' bằng AB'+ AC’ + B'C'= B'D+C’E+ B'C' (2)
Vì DE ≤ B'D + C’E+ B'C' (dấu bằng xảy ra khi B' trùng B, C' trùng C) nên chu vi của ∆ ABC ≤ chu vi của ∆ A'B'C'
Vậy ∆ ABC có chu vi bé nhất.
Đúng 1
Bình luận (0)
Cho A nằm trong góc xOy, B thuộc Ox, C thuộc Oy. xác đinh vị trí điểm B,C sao cho tam giác ABC có chu vi nhỏ nhất
Cho góc nhọn xOy, điểm A nằm trong góc đó. Dựng điểm B thuộc tia Ox, điểm C thuộc tia Oy sao cho tam giác ABC có chu vi nhỏ nhất.
Cho góc nhọn xOy, điểm A nằm trong góc đó. Dựng điểm B thuộc tia Ox, điểm C thuộc tia Oy sao cho tam giác ABC có chu vi nhỏ nhất ?