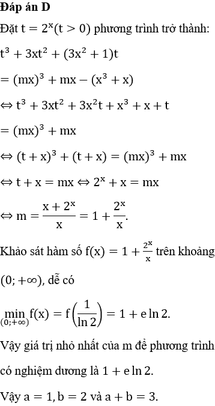Tìm số nguyên x để x3+3x2+3x+9 nhận giá trị là số nguyên tố

Những câu hỏi liên quan
2. Tìm giá trị nguyên của x để biểu thức B = x3 + 3x2 + 3x + 9 nhận giá trị là số
nguyên tố.
Ta có: \(B=x^3+3x^2+3x+9\)
\(=x^2\left(x+3\right)+3\left(x+3\right)\)
\(=\left(x+3\right)\left(x^2+3\right)\)
Để B là số nguyên tố thì: \(\left[{}\begin{matrix}x+3=1\\x^2+3=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x^2=-2\left(voli\right)\end{matrix}\right.\)
Thay \(x=-2\) vào B ta được:
\(B=\left(-2+3\right)\left[\left(-2\right)^2+3\right]=7\) là số nguyên tố.
Vậy \(x=-2\)
Đúng 0
Bình luận (0)
Tìm giá trị thực của m để hàm số
F
x
x
3
-
2
m
-
3
x
2
-
4
x
+
10
là một nguyên hàm của hàm số
f
x
3
x
2
-
12
x
-
4
với mọ...
Đọc tiếp
Tìm giá trị thực của m để hàm số F x = x 3 - 2 m - 3 x 2 - 4 x + 10 là một nguyên hàm của hàm số f x = 3 x 2 - 12 x - 4 với mọi x ∈ R
A. m = 3 2
B. m = - 9 2
C. m = 9 2
D. m = 9
Cho n là số tự nhiên .Tìm UCLN và BCNN của n và n+2
b) Tìm các giá trị nguyên x để y nhận đc giá trị nguyên ,Biết y=5x+9/x3
Cho B = x^3 + 3x^2 + 3x + 9
Tìm giá trị của x để B là số nguyên tố
Ta có: \(B=x^3+3x^2+3x+9=x^2\left(x+3\right)+3\left(x+3\right)\)
\(\Rightarrow B=\left(x+3\right)\left(x^2+3\right)\)
Để B là số nguyên tố => phải có một số bằng 1
Vì \(x^2\ge0\Rightarrow x^2+3\ge3>1\)
\(\Rightarrow x+3=1\Rightarrow x=1-3=-2\)
Vậy x = -2
Đúng 0
Bình luận (0)
B = (x+3).(x^2+3)
Để B là số nguyên tố => x+3 = 1 hoặc x^2+3 = 1
=> x=-2
Khi đó : B = 1.(4+3) = 7 là số nguyên tố (tm)
Vậy x=-2
k mk nha
Đúng 0
Bình luận (0)
Tìm giá trị thực của m để hàm số F(x) x3 – (2m – 3)2 – 4x + 10 là một nguyên hàm của hàm số f(x) 3x2 – 12x – 4 với mọi
x
∈
ℝ
A.
m
3
2
B.
m
-
9
2
C.
m
9
2
D.
m...
Đọc tiếp
Tìm giá trị thực của m để hàm số F(x) = x3 – (2m – 3)2 – 4x + 10 là một nguyên hàm của hàm số f(x) = 3x2 – 12x – 4 với mọi x ∈ ℝ
A. m = 3 2
B. m = - 9 2
C. m = 9 2
D. m = 9
Số thực m nhỏ nhất để phương trình
8
x
+
3
x
.
4
x
+
(
3
x
2
+
1
)
2
x
(
m
3
-
1
)
x
3
+
(
m
-
1
)...
Đọc tiếp
Số thực m nhỏ nhất để phương trình 8 x + 3 x . 4 x + ( 3 x 2 + 1 ) 2 x = ( m 3 - 1 ) x 3 + ( m - 1 ) x có nghiệm dương là a + eln b, , với a,b là các số nguyên. Giá trị của biểu thức a + b bằng
A. 7
B. 4
C. 5
D. 3
Số thực m nhỏ nhất để phương trình
8
x
+
3
x
.
4
x
+
(
3
x
2
+
1
)
2
x
(
m
3
-
1
)
x
3
+
(
m
-
1
)
x...
Đọc tiếp
Số thực m nhỏ nhất để phương trình 8 x + 3 x . 4 x + ( 3 x 2 + 1 ) 2 x = ( m 3 - 1 ) x 3 + ( m - 1 ) x có nghiệm dương là a+e lnb, với a,b là các số nguyên. Giá trị của biểu thức a+b bằng
A. 7.
B. 4.
C. 5.
D. 3.
Số giá trị nguyên của hàm số m để hàm số
y
x
3
-
3
x
2
+
m
có 5 điểm cực trị là A. 3 B. 4 C. 6 D. 5
Đọc tiếp
Số giá trị nguyên của hàm số m để hàm số y = x 3 - 3 x 2 + m có 5 điểm cực trị là
A. 3
B. 4
C. 6
D. 5
Chọn A.
Hàm số y = x 3 - 3 x 2 + m có 5 điểm cực trị
⇔ hàm số y = x 3 - 3 x 2 + m có 2 điểm cực trị nằm về 2 phía của trục Ox
Xét hàm số y = x 3 - 3 x 2 + m
ta có: y ' = 3 x 2 - 6 x = 0
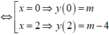
Hàm số y = x 3 - 3 x 2 + m có 2 điểm cực trị nằm về 2 phía của trục Ox
![]()
⇔ 0 < m < 4
Lại có m ∈ ℤ ⇒ m ∈ 1 ; 2 ; 3
Đúng 0
Bình luận (0)
Số giá trị nguyên của tham số m để hàm số
y
x
3
-
3
x
2
+
m
có 5 điểm cực trị là
Đọc tiếp
Số giá trị nguyên của tham số m để hàm số y = x 3 - 3 x 2 + m có 5 điểm cực trị là
![]()
![]()
![]()
![]()